java创建数组

1
2
3
4
5
6
7
8
9
10
double[] a;//声明数组
int N = 100;
a = new double[N];
for (int i = 0;i < N;i++) {
	a[i] = 0.0;//初始化！
}
//也可以用简单写法
double[] b = new double[N];
//或者直接声明初始化
double[] c = {1,2,3,4,5,6};

找到最大值

伪代码

1
2
3
4
5
6
对于一个数组a[n]
max = 0
for i in range(length(a[n])):
	if (a[i] > max):
		max = a[i]
return max

我们用java来实现一下

1
2
3
4
5
6
7
8
9
10
int N = 100;
double[] a = new double[N];//声明数组
for (int i = 0;i < N;i++) {
	a[i] = i;
}
double max = 0;
for (int i = 0;i < N;i++) {
	if (a[i] > max) max = a[i];
}
StdOut.println(max);

颠倒数组顺序

先来看伪代码

1
2
3
4
5
6
7
对于一个数组a[n]，颠倒顺序。
int temp;
for i in range(a.length):
	temp = a[i]
	a[i] = a[n-1-i];//因为n-1才是最后一个数的index
	a[n-1-i] = temp;
return a[n]

我们用java来实现一下

1
2
3
4
5
6
7
8
9
10
11
12
int N = 100;
double[] a = new double[N];
for (int i = 0;i < N;i++) {
	a[i] = i;
}
double temp = 0;
for (int i = 0;i < N;i++) {
	temp = a[i];
	a[i] = a[n-1-i];
	a[n-1-i] = temp;
}
StdOut.println(a);

矩阵乘法

首先我们用伪代码实现

1
2
3
4
5
6
对于两个二维矩阵a[M][N]和b[N][P]
for i in range(M):
	for j in range(P):
		for k in range(N):
			c[i][j] = a[i][k] * b[k][j]
return c[M][P]

下面用java实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int N = 100;
int[][] a = new int[N][N];
for (int i = 0;i < N;i++) {
	for (int j = 0;j < N;j++) {
		a[i][j] = i*10 + j;
	}
}
//然后再初始化b，之后开始乘法
int [][] c = new int[N][N];
for (int i = 0;i < N;i++) {
	for (int j = 0;j < N;j++) {
		for (ing k = 0;k < N;k++ ) {
			c[i][j] = a[i][k] * b[j][k];
		}
	}
}
StdOut.println(c);

牛顿法求平方根

首先我们用伪代码来实现，我们知道

1
2
3
4
5
6
所以伪代码就是
error = 1e-15
x = a
while(abs(x - a/x) > error):
	x = 0.5*(x + a/x)
return x#这样也就是当误差小于error的时候就结束运算了。

下面用java来实现

1
2
3
4
5
6
7
8
9
if(a < 0) {
	return Double.NaN;
}
double error = 1e-15;
double x = a;#这里是随便赋值，因为反正都要送进去迭代
while(Math.abs(x - a/x) > error) {
 x = (x + a/x) / 2.0;
}
return x;

二分查找

我们先来写一下算法的伪代码

1
2
3
4
5
6
7
8
9
10
11
显然对于一个已经按照次序排好序的数列a[n]，我们要找到给定数列值key在数列中的位置。
lo = start_index
hi = end_index
while lo <= hi:
	mid = lo + (hi - lo) / 2
	if(key < a[mid]):
		hi = mid - 1
	else if key > a[mid]:
		lo = mid + 1
	else:
		return mid

下面用java来实现一下

1
2
3
4
5
6
7
8
9
10
11
public static int rank(int key, int[] a) {
	int lo = 0;
	int hi = a.length - 1;
	while(lo <= hi) {//必要条件
		int mid = lo + (hi - lo) / 2;
		if (key < a[mid]) hi = mid - 1;
		else if (key > a[mid]) hi = lo + 1;
		else return mid;
	}
	return -1;
}

java数学库中的方法

image-20230528002906266

下面是StdRandom库和StdStats中的一些基本方法

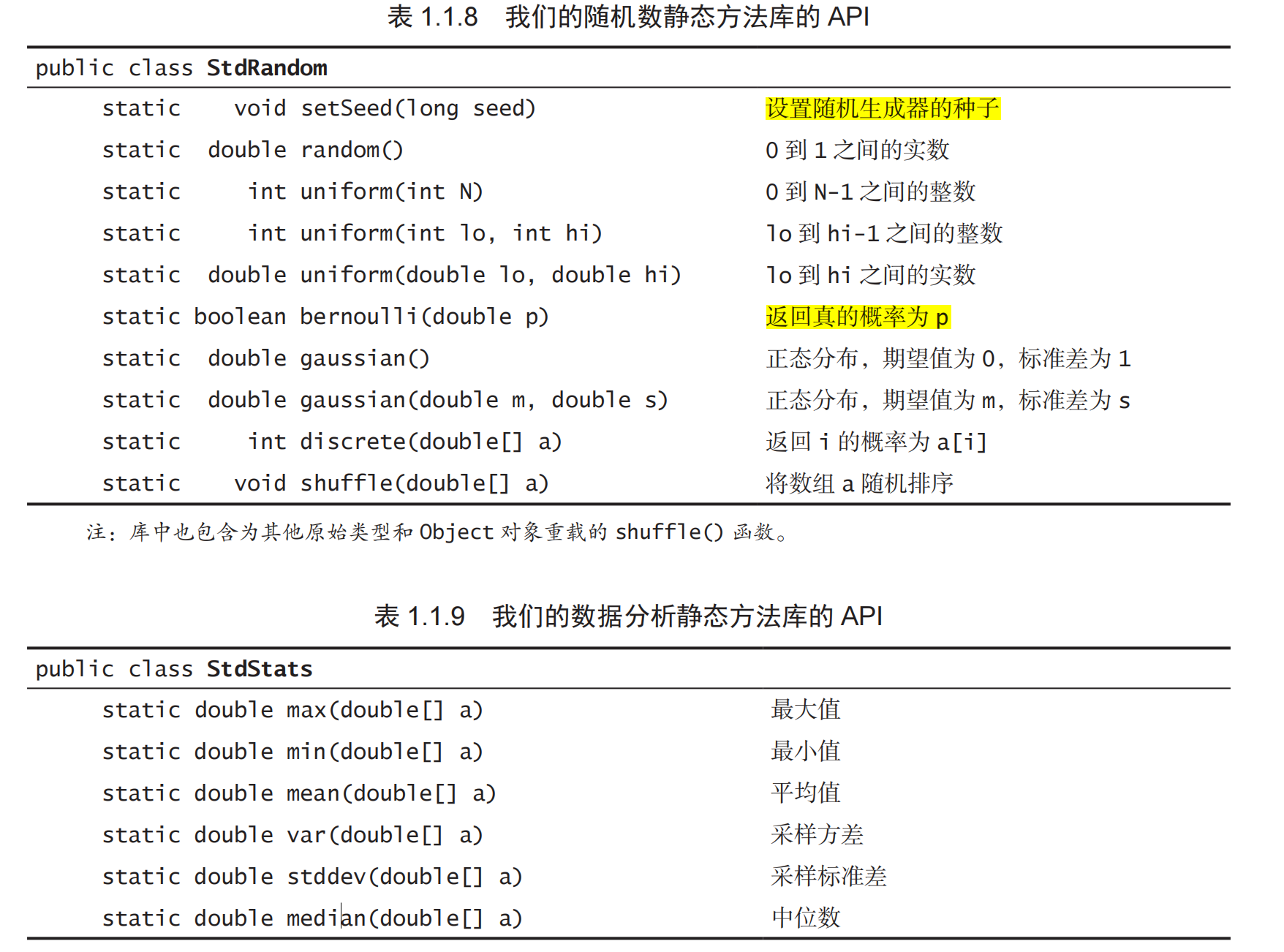
image-20230528002945970

下面实现一些练习

随机返回[a,b)之间的一个double值

1
2
3
4
public static double uniform(double a, double b)
{
	return a + StdRandom.random()*(b-a);
}

随机返回[0, N)之间的一个int值

1
2
3
4
public static int uniform(int N)
{
	return (int) (StdRandom.random()*N);
}

根据离散概率随机返回的int值(出现i得概率为a[i])(非常重要的算法！)

1
2
3
4
5
6
7
8
9
10
11
12
13
public static int discrete(double[] a)//显然我们知道a[i]中的和为1
{
	double r = StdRandom.random();//取一个0,1之间的随机数
	double sum = 0.0;
	for(int i=0;i < a.length;i++) {
		sum = sum + a[i];
		if(sum >= r) return i;
	}
	return -1;
}
这个我们要好好理解一下，因为r是一个均匀分布在0,1上，所以这里的i就相当于r一样，我们比如说a[n]=[0.2,0.3,0,5]
那么显然0.5的概率最大，也就是取i=2的概率应该最大，其实就是我们选取r的时候，r落在后面的概率就大，比如r>0.5时，就要把三个概率全加上就满足，这时候就返回2，所以说全加上的概率就是返回2的概率，而恰好全加上的概率就是r>0.5的概率，也就是0.5，恰好相等。
再举个例子，比如r>0.2且r<0.5，我们想要返回i=1，那么我们想要返回i=1的概率是0.3，如何实现呢，其实也就是概率分布的p(X<x)=0.2+0.3注意这里此时x=2这样就能保证X的取值不可能返回2，但是返回0，1两个，这也不行，我们要他只返回值为1，不返回0，所以还要再限制X的范围到X>0,而再前面的p(X<=0)的概率我们都知道了是X=0的概率也就是0.2，所以取X=1的概率就是0.3

随机将double数组中的元素排序

1
2
3
4
5
6
7
8
9
10
public static int shuffle(double[] a)
{
	int N = a.length;
	for(int i = 0;i < N;i++) {
		int r = i + StdRandom.uniform(N-i);//显然范围是[i, N-1]
		double temp = a[i];
		a[i] = a[r];
		a[r] = temp;//即将a[i]与[i,N-1]中的任意一个元素进行交换，就实现了随机排序，打乱的效果。
	}
}