图像处理（3）均值滤波

import cv2 as cv
import numpy as np

图像滤波（低通滤波）

img = cv.imread("def.jpg", cv.IMREAD_COLOR)
cv.imshow('img', img)
cv.waitKey(0)
cv.destroyAllWindows()

卷积原理

下面说一下卷积的原理。

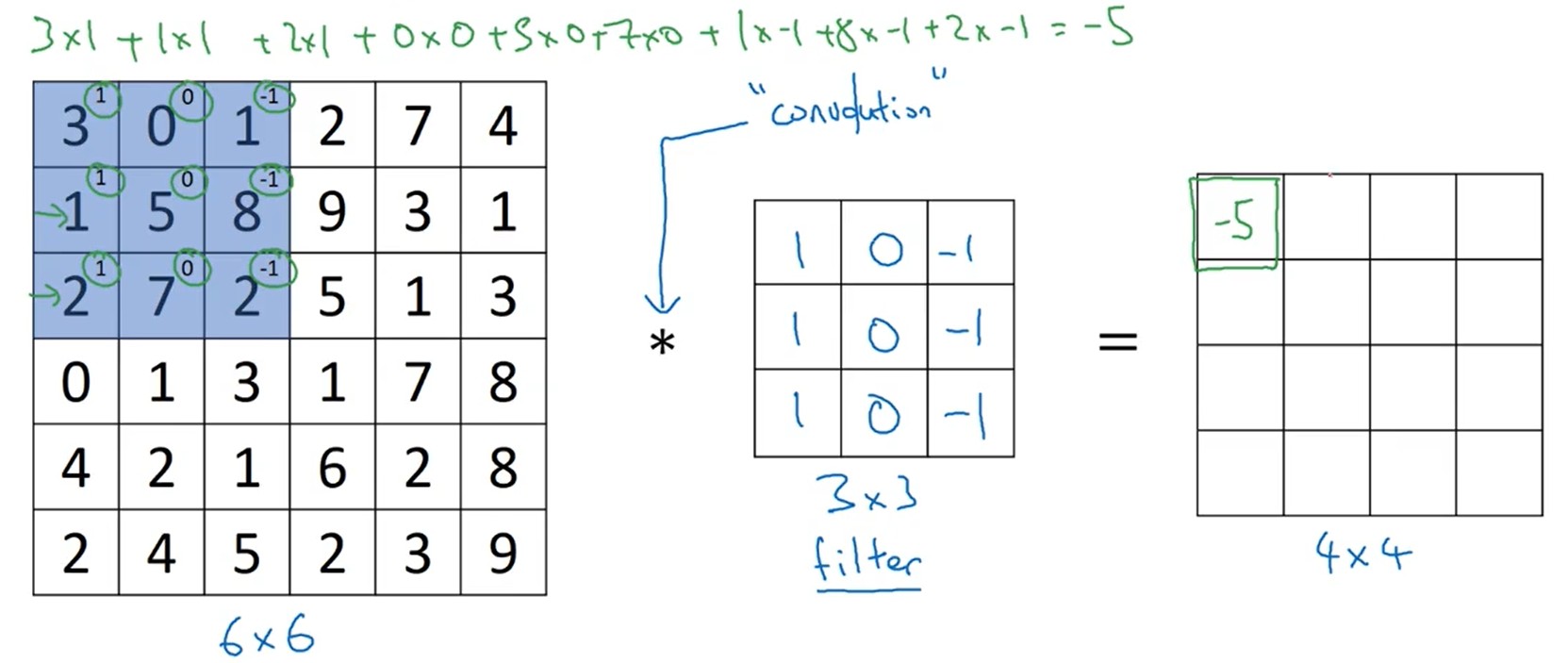
显然，就是拿一个小矩阵在大矩阵上做点积乘法，得到一个值代替原来的像素。所以对于$n\cdot n$的矩阵，假设卷积核shi$m\cdot m$那么卷积之后的结果矩阵大小为$(n-m+1)\cdot (n-m+1)$，如图所示，卷积用来提取特征。

参数还有步长，也就是卷积核每次移动的单位。上面例子默认为1，如果步长为p，那么最终卷积结果的大小为

$$[\frac{(n-m) + 2p}{p}]$$

可以带入尝试，结果正确，下面是代码。

blur = cv.blur(img, (5, 5))#进行平滑处理
cv.imshow('blur', blur)
cv.waitKey(0)
cv.destroyAllWindows()#简单滤波

滤波可以消除高斯噪声，椒盐噪声。

• 椒盐噪声：随机出现的「纯白点」或者「纯黑点」

效果如图所示：

我们从图中可以看出，用卷积运算起到了提取关键信息的作用。

对于上述均值滤波，其意义为字面意思，即取均值，那么卷积核应如下：

$$K = \alpha \begin{bmatrix} 1 & 1 \cdots 1\\ 1 & 1 \cdots 1\\ 1 & 1 \cdots 1\\ \end{bmatrix}_{m\times m}$$

这里显然，卷积之后每个元素相当于原来$m\times m$个元素的和的均值！所以系数$\alpha = \frac{1}{m^2}$

对于这个元素全是1的矩阵来说，起到了正交化的作用。正交化的方盒滤波也成为均值滤波。

#方框滤波
box = cv.boxFilter(img, -1, (5, 5), normalize=True)#这里如果是false可能会出现全黑，所以我用True
#-1 represents the depth of the image, which is same as the previous image.
#normalize=False means not to normalize to 1, which may cause pixel exceeding the threshold.
cv.imshow('box', box)
cv.waitKey(0)
cv.destroyAllWindows()

高斯滤波

首先，高斯滤波一定是基于高斯分布的，而图像一般有宽和高两个方向，即二维坐标(x, y)。所以我们考虑二维高斯概率密度函数

$$f(x, y) = (2\pi \sigma_1\sigma_2\sqrt{1-\rho^2})^{-1}exp[-\frac{1}{2(1-\rho^2)}(\frac{(x-\mu_1)^2}{\sigma_1^2} - \frac{2\rho(x-\mu_1)(y - \mu_2)}{\rho_1\rho_2} + \frac{(y-\mu_2)^2}{\sigma_2^2})]$$

其中$\mu_1, \mu_2$是x, y的均值，$\sigma_1, \sigma_2$是x, y的标准差，$\rho$是x, y的相关系数！

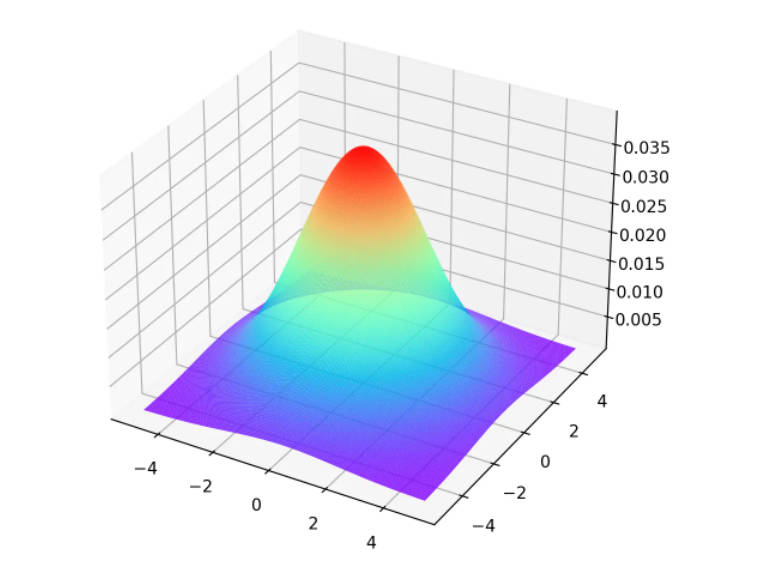
因为二维高斯分布公式十分复杂，所以假设$\mu_1 = \mu_2 = 0, \rho = 0$，公式化简为

$$f(x, y) = \frac{1}{2\pi\sigma_1\sigma_2}exp[-\frac{1}{2}(\frac{x^2}{\sigma_1^2} + \frac{y^2}{\sigma_2^2})]$$

这样一看十分简便了。我们假设卷积核中心坐标(x, y) = (0, 0)那么整个卷积核矩阵可以写作

$$K = \begin{bmatrix} (-1, 1) & (0, 1) & (1, 1) \\ (-1, 0) & (0, 0) & (1, 0)\\ (-1, -1) & (0, -1) & (1, -1)\\ \end{bmatrix}$$

将坐标值带入简化后的二维高斯分布概率密度函数，并且取$\sigma_1 = \sigma_2 = 1.5$

可以算出一个概率密度矩阵，矩阵每个元素的位置就是二维坐标，我们用归一法得到概率值。也就是每个元素除以K的元素和，得到高斯模板卷积核。下面是代码。

#高斯滤波
gaussian = cv.GaussianBlur(img, (5, 5), 1)#高斯滤波按照近大远小来分配权重
#画图的部分我们都给他换成matplotlib中的函数！
plt.imshow(gaussian)
plt.title('gaussian')
plt.axis("off")
plt.show()

可以看到提取的特征更加明显。

中值滤波

#中值滤波
median = cv.medianBlur(img, 5)#中值滤波
#效果并没有高斯滤波好，但是处理噪音很好
plt.imshow(median)
plt.show()

对卷积核框住的像素值进行排序；取中间值作为输出结果。代码在上方，效果如图所示：

#显示所有的
res = np.hstack((img, blur, box, gaussian, median))#将多个图像水平拼接在一起形成一个新的图像
plt.imshow(res)
plt.show()

双边滤波

高斯滤波在去除高斯噪声的同时，并没有保护边缘，所以我们用双边滤波保护边缘。我们可以通过相邻像素做差，就可以标记出边缘，差值越大，标记出边缘的可能性越高。它考虑了像素之间的空间距离和像素值的差异，以保留图像中的边缘信息。

我们用一张图简单解释其原理。

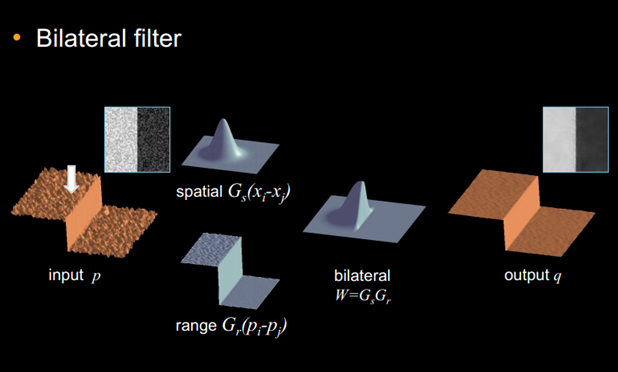
传统滤波器（也可以考虑高斯滤波器）

假设给定了像素中心点，那么这个点的像素会被写在矩阵的中心，在其周围表示了周围坐标点的像素。

我们知道，在卷积核中，每个元素表示相应位置的权重，在加权求和的时候，我们想要哪个位置的像素对最终结果的影响大一些，那我们就在卷积核中让相应位置的权重变大，那么如果想要保留一个图像的细节，当然要将其原来的像素值权重设置得很大，而距离原来点越远的点的像素，所占比重应该越来越小，这就是传统滤波器的核函数效果（高斯滤波器就是如此），我们也称其权重分布为空间上的权重分布(spatial)，如上图Gs。

那么对于保边(edge preversing)滤波器，或者说双边滤波器，我们来看上图，原图是黑白分界，中间看出一条分界线，如果用高维矩阵进行卷积，很容易就把边一起融合掉了，因为滤波器（加权计算）本身就有模糊噪声的作用。我们想要保住这条分界线，就要考虑第二种权重分布，值域上的权重分布(range)，如上图Gr。

值域上的权重分布就是周围像素与中心像素值差越大，那么权重就越小。所以，比如上图中，中心像素在分界线左侧，那么中心点左边的像素值就和他相近，所以分界线左侧的点，权重就大，影响着分界线左侧滤波之后的结果。中心点右边的像素值与中心点像素值差值很大，那么权重就小，所以最后中心点的像素值就主要是左边。

最终的卷积核就是两者函数相乘，$W = G_s \times G_r$（矩阵点乘）得到最终的核函数。

我们来看一下计算。

$G_s(p)$为高斯概率密度函数，卷积核中心点q, 像素坐标$(x_q, y_q)$，卷积核中任意点p, 像素坐标$(x_p, y_p)$。

$$\begin{align} G_s(p) &= exp(-\frac{||p-q||^2}{2\sigma_s^2})\\ &= exp(-\frac{(x_p - x_q)^2 + (y_p - y_q)^2}{2\sigma_s^2}) \end{align}$$

$G_r(p)$灰度值距离权重，同理我们也用指数函数。卷积核中心点像素计作$I_q$，积核中某一像素$I_p$。

$$G_r(p) = exp(-\frac{||I_p - I_q||^2}{2\sigma_r^2})$$

然后对应项相乘即可！

$$W = \sum_{p \in K}G_s(p)G_r(p)$$

得到最终的双边卷积核。

显然其中的$\sigma_r$参数越大，像素差值的影响就越大。同理，$\sigma_s$越大，点之间距离的影响就越大。

代码如下：

bifilter = cv.bilateralFilter(img, 5, sigmaColor=30, sigmaSpace=30)
plt.imshow(bifilter)
plt.show()

可以看出，边界被很好的保留。