crypto基础：数论（一）群环域的引入

今天开始，我将我掌握的数论内容，经过大脑的排版，以通俗易懂的方式记下。

环的引入

Definition

我们先从以环定义一个集合

$$\mathbb{Z}/m\mathbb{Z} = \{0,1,2,3,...,m-1 \}$$

我们把这个符号称作模m的环。

很形象的理解，环嘛，就是转一圈。有限制的，到m-1就回来了。我们将环中的任意元素相加，相乘，结果再模m就会得到我们环中的元素，这就是说，怎样都无法出圈了。

如图：

$$\begin{tabular}{|c|c|c|c|c|c|} \hline + & 0 & 1 & 2 & 3 & 4\\ \hline 0 & 0 & 1 & 2 & 3 & 4\\ \hline 1 & 1 & 2 & 3 & 4 & 0\\ \hline 2 & 2 & 3 & 4 & 0 & 1\\ \hline 3 & 3 & 4 & 0 & 1 & 2\\ \hline 4 & 4 & 0 & 1 & 2 & 3\\ \hline \end{tabular}$$

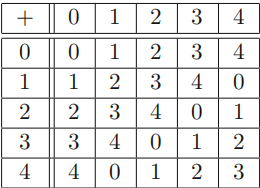
表格中是一个模5的环$\mathbb{Z}/5\mathbb{Z}$

并且给出了全部的加法和乘法模5之后的结果，意料之中！

有了环的定义，就有了它的缩减版的定义，我们来看新定义

Definition

我们知道a有一个逆m的充分必要条件是当且仅当$gcd(a,m)=1$。我们把有逆的数称作单位元，那么所有单位元的集合我们表示为：

$$\begin{align} &(\mathbb{Z}/m\mathbb{Z})^* = \{a\in \mathbb{Z}/m\mathbb{Z}:gcd(a,m)=1\}\\ & = \{a\in \mathbb{Z}/m\mathbb{Z}:a\ \text{has an inverse module m}\} \end{align}$$

我们称其为m的单位群。

举个例子

$$(\mathbb{Z}/24\mathbb{Z})^* = \{1,5,7,11,13,17,19,23\},\ 确实是和24互素的数$$

有趣的性质是，我们对单位元的两个元素相乘然后去模m，仍然得到一个单位元。

比如上面这个模24的单位群，大家可以用我上面列表的方式试一试，结果同理。

注意，这个加了星号的符号，把0去掉了，很容易理解，0肯定是没有逆的。

下面引入欧拉函数

Definition

欧拉函数我们表示成

$$\phi(m) = \#(\mathbb{Z}/m\mathbb{Z})^* = \#\{0 \le a \lt m:gcd(a,m)=1\}.$$

其实就是表示的上面单位群里面，满足条件的单位元的个数。

当m用唯一分解定理表示成$m = p_1^{s_1}p_2^{s2}…p_n^{s_n}$时，

欧拉函数的公式我们写为：

$$\phi(m)=m\prod_{i=1}^n(1-\frac{1}{p_i})$$

我们继续讨论上面的模的单位群。

如果模数p是一个素数，那么

$$(\mathbb{Z}/p\mathbb{Z})^* = \{1,2,3,...,p-1\}.$$

这是显然的，因为每个数都和素数互素。

当我们把0从模p的环里面拿出去之后，剩下的单位元，是对乘法封闭的，也就是互相乘法运算再模p，得到的仍然是模p的这个单位群里面的元素。

Definition

如果p是素数，那么模p的环$\mathbb{Z}/p\mathbb{Z}$中的元素，以及它们之间的加减乘除运算法则，就是一个域(field)的例子。

域是一个交换环的通用名称，这个交换环里每个非0的元素都要有乘法逆。我们其实对一些域很熟悉，比如$\mathbb{R}$,$\mathbb{Q}$等。

模p的域$\mathbb{Z}/p\mathbb{Z}$

只有有限个元素，它也被称为有限域，实际上这个词更通用，记为$\mathbb{F}_p$

所以上述两个符号只是同一种东西的不同记法。有一点区别就是$\mathbb{F}_p$是域，从定义上扣，域是带运算法则的。

同理，模p的单位群，加上它的运算法则，也就是模p的域，记作$\mathbb{F}_{p}^*$

有限域是密码学的基础。

我们现在有一个初步的认识了，群环域。