Information Retrieval basis

Precision and Recall

We use precision and recall as the measurements to estimate the efficiency of a retrieval system.

Now there is a ‘contingency’ table.

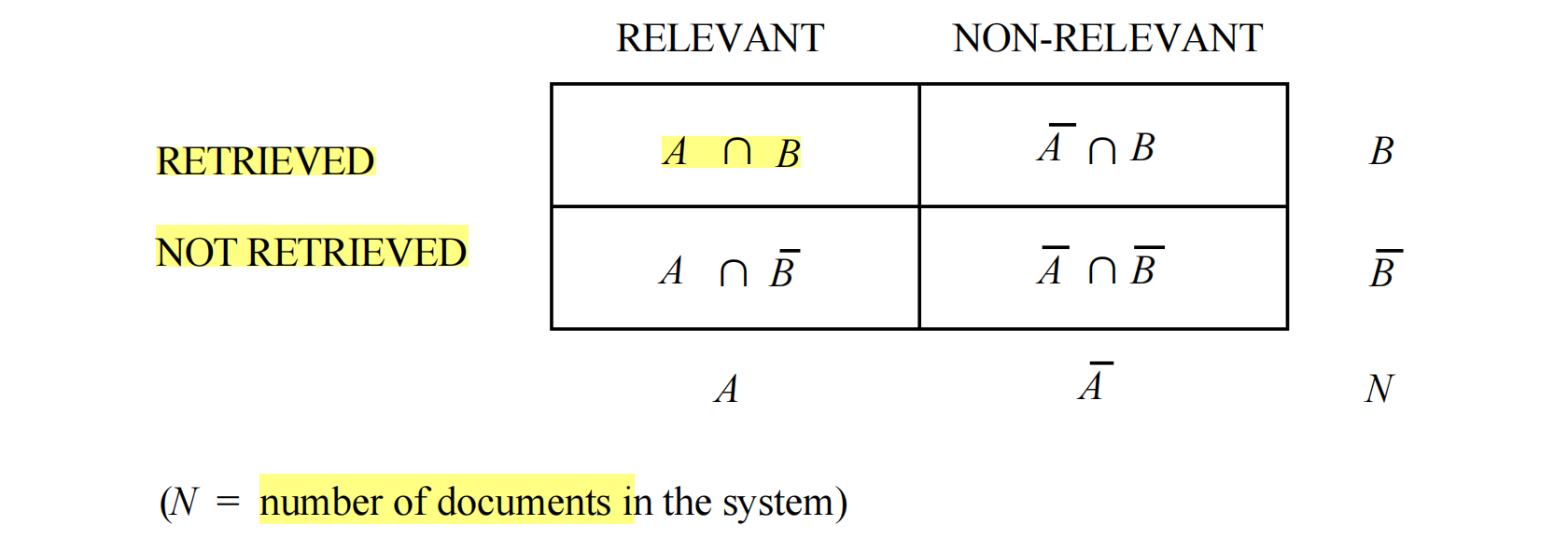
and now we define the measurements using formulas.

$$& PRECISION = \frac{|A\cap B|}{|B|} \\ & RECALL = \frac{|A\cap B|}{|A|} \\ & FALLOUT = \frac{|\overline {A} \cap B|}{|\overline A|}$$

and There is a function relationship between all three involving a parameter called generality(G), which is a measure of the density of the relevant documents in the collection. The relationship is

$$P = \frac{R \times G}{(R \times G) + F(1-G)} \ \ \ \ \ where\ G = \frac{|A|}{N}$$

If the output of the strategy depends on a patameter, such as rank position or co-ordination level(number of terms in a query in common with a document), the Precision and Recall will vary depending on the parameter, forming $(P(\lambda), R(\lambda))$

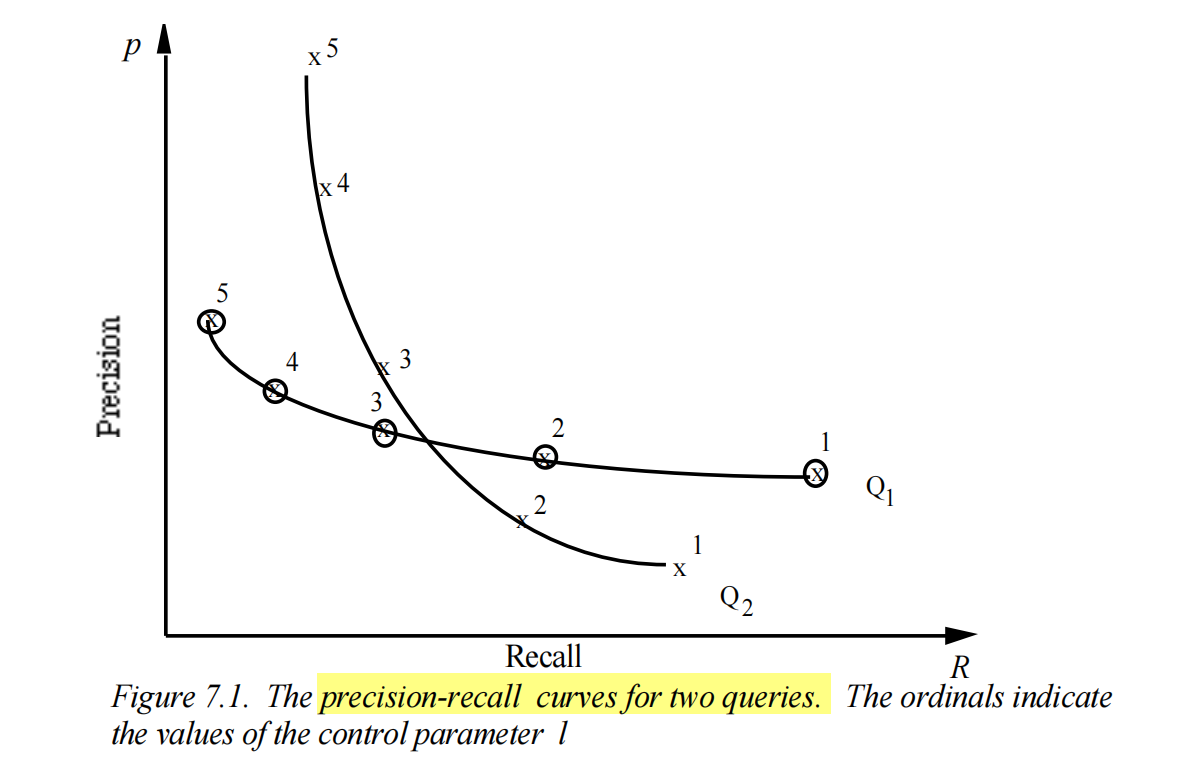
There are some terms like g-index and h-index.

g-index

$$g = \max_k(\sum_{i = 1}^k f(i) > k^2)$$

We can see this formula, and we choose top k papers and calculate its ciataions, when the number of citations exceeds $k^2$, we say the g-index of this author is k, also called g.

In conclusion, if we are given a set of papers ranked in decreasing order of the number of citations that they received, then g-index is the unique largest number such that the top g papers together received at least $g^2$ citations.

h-index

$$h = \max_i \min(f(i), i)$$

As for h-index, if we choose top i papers(i is the rank of citations of papers), $f(i)$ represents the number of the ith paper’s citations.

So firstly we know if i is very small(the highest ranking of citations), then $f(i)$ will be large. As i increases, $f(i)$ will decrease, however, as long as $f(i) > i$ , the function of h will return i. When $f(i) < i$ the function will return $f(i)$ , but at this moment $f(i)$ is not very large and $f(i)$ is still decreasing! Thus we just choose the $i$ which just doesn’t exceed the corresponding $f(i)$. Mathematicscally it is not very accurate.

In conclusion, An author has index h if h of his/her N papers have at least h citations each, and the other (N-h) papers have no more than h citations each.