我们平时的key, cer等等密钥文件，打开时并不是我们喜欢的n,p,q的公私钥形式，而是已经编码好的形式，而编码的规则就是基于X.690标准中的ASN.1的编码格式：Basic Encoding Rules(BER), Canonical Encoding Rules(CER), Distinguished Encoding Rules(DER).

The BER were origin rules laid out by the ASN.1 standard for encoding data into a binary format.The rules used octets(8bit bytes) to encode data.

X.680 defines a syntax for declaring data types, for example: booleans, numbers, strings and compound structures. Each type definition also includes an identifying number.

X.680 defined several primitive data types, like BooleanType, IntegerType, OctetStringType. Types are associated with a class. For example, the primitive types are part of the universal class. There are other classes, including application, private and context-specific, which are used to specific applications.

Conbined, the class and type from a tag, which therefore corresponds to a unique data definition. X.690 rules are for encoding those tags, data values, and the lengths of that encoded data.

BER encoding

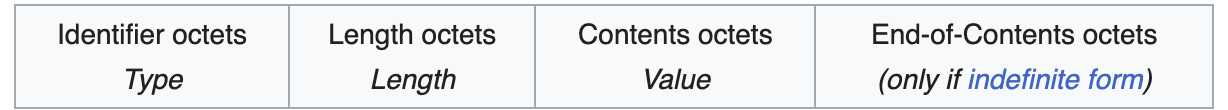
image-20230822012505668

This is the structure of BER encoding including three or four components. Note that if a Length is zero, namely there are no Contents octets, e.g. the NULL type. The End-of-Contents octets are only used for the indefinite form of Length.

openssl

This note is from the book \.

If we want to check the version of openssl, because sometimes a wrong version will cause the error.

1
openssl version -a

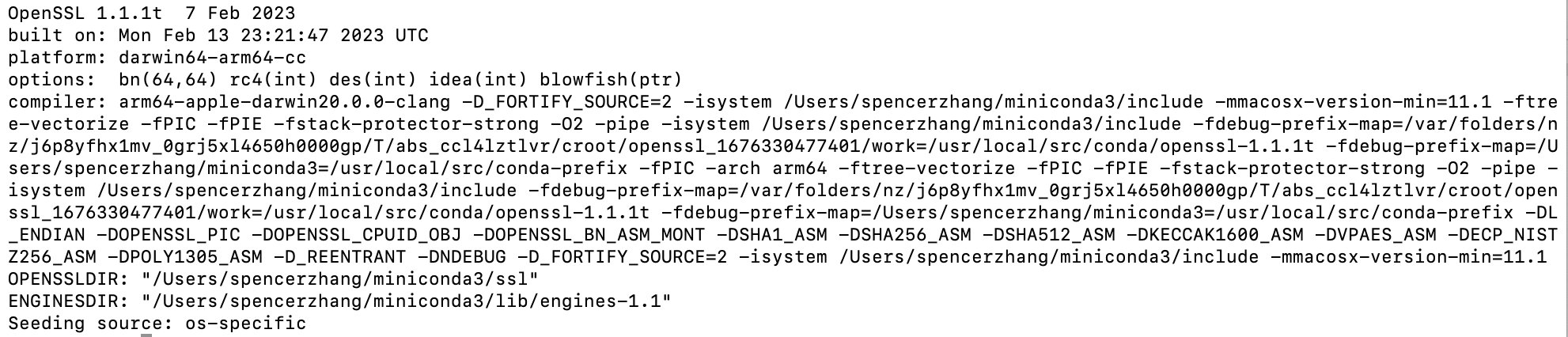
image-20230822021244702

you will find how your OpenSSL was compiled and where is the OPENSSLDIR, which tells you where OpenSSL looks for its default configuration and root certificates.

building OpenSSL

we can download it and build it by ourselves

1
2
3
4
5
6
 ./config \
--prefix=/opt/openssl \
--openssldir=/opt/openssl \
no-shared \
-DOPENSSL_TLS_SECURITY_LEVEL=2 \
enable-ec_nistp_64_gcc_128

—prefix makes sure to install OpenSSL to a private location that doesn’t clash with the system-provided version.

The other important option is no-shared, which doesn’t use static linking and makes self-contained command-line tools.

then we can build

1
2
3
make
make test
sudo make install

we can use ‘man’ to learn specific utility.

1
man openssl-ciphers# will give you detailed information on how cipher suites are configured.

or 

1
man openssl-enc

Build a trust store

The trust store is a collection of trusted root certificates.OpenSSL doens’t come with a trust store, so you can use it built into your operating system.

In ubuntu, you can use update-ca-certificates to replace the contents of the /etc/ssl/certs

Mozila put a lot of effort to maintaining a transparent and up-to-date root store for use in Firefox. It is opensource

1
https://hg.mozilla.org/releases/mozilla-beta/file/tip/security/nss/lib/ckfw/builtins/certdata.txt

Unfortunately its certificate collection is in a proprietary format, which is not of much use to others as is. To convert Mozila’s root store, we download

1
https://raw.githubusercontent.com/curl/curl/master/scripts/mk-ca-bundle.pl

it will fetch the certificate data from Mozilla and convert it into the PEM format.

1
./mk-ca-bundle.pl

key and Certificate Management

Users wish to configure and run a web server that supports SSL. That process consists of three steps: 

1
2
3
(1)generate a private key
(2)create a Certificate Signing Request(CSR) and sent it to a CA.
(3)install the CA-provided certificate in your web server.

Key Generation

key algorithm: we usually use RSA and ECDSA in our certificates.

key size: the default for RSA keys used to be 512 bits,which is insecure. Today, 2048-bit RSA are considered secure, or 256 bits for ECDSA.

Passphrase: using a passphrase with a key is optional, but recommended

To generate an RSA key, we use genpkey

1
2
3
4
5
openssl genpkey -out fd.key \ 
-algorithm RSA \
-pkeyout rsa_keygen_bits:2048 \
-aes-128-cbc
#then run this and then input our passphrase for the key.

Here I specific that the key be protected with AES-128. You can also use AES-256(with -aes-256-cbc)

Note: By default, OpenSSL will set the public exponent of new rsa to 65537.

When we use the genpkey command, the generated private keys are stored in PKCS #8 format, which is jest text

1
cat fd.key

and if we want to see the detailed data like n and e in the private key, the command can be

1
openssl pkey -in fd.key -text -noout

the the datas will be exhibited.

If you only want to have the public part of a key, the command can be

1
openssl pkey -in fd.key -pubout -out fd-public.key

The process is similar for ECDSA keys

1
2
3
4
 openssl genpkey -out fd.key \
-algorithm EC \
-pkeyopt ec_paramgen_curve:P-256 \
-aes-128-cbc

for web server keys, you are generally limited to only two curves that are widely supported: P-256 and P-384.

The recent additions ed25519 and so on are also supported, but they are different types of curves and have to be specified using the -algorithm switch

1
openssl genpkey -algorithm ed25519

python cryptography algorigthm

note: Contents are from my accumulating writeups of many CTF competitions.

hex replacement bruce

This is a easy rsa that some letters of the p are substituted in terms of ‘FC’, the ‘FC’ may be the same in the previous p, and also can be ‘9F’ in the previous p.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import subprocess
from Cryptodome.Util.number import *
from gmpy2 import *
import itertools

p_inil = "DCC5A0BD3A1FC0BEB0DA1C2E8CF6B474481B7C12849B76E03C4C946724DB577D2825D6AA193DB559BC9DBABE1DDE8B5E7805E48749EF002F622F7CDBD7853B200E2A027E87E331AFCFD066ED9900F1E5F5E5196A451A6F9E329EB889D773F08E5FBF45AACB818FD186DD74626180294DCC31805A88D1B71DE5BFEF3ED01F12678D906A833A78EDCE9BDAF22BBE45C0BFB7A82AFE42C1C3B8581C83BF43DFE31BFD81527E507686956458905CC9A660604552A060109DC81D01F229A264AB67C6D7168721AB36DE769CEAFB97F238050193EC942078DDF5329A387F46253A4411A9C8BB71F9AEB11AC9623E41C14FCD2739D76E69283E57DDB11FC531B4611EE3"
n = 719579745653303119025873098043848913976880838286635817351790189702008424828505522253331968992725441130409959387942238566082746772468987336980704680915524591881919460709921709513741059003955050088052599067720107149755856317364317707629467090624585752920523062378696431510814381603360130752588995217840721808871896469275562085215852034302374902524921137398710508865248881286824902780186249148613287250056380811479959269915786545911048030947364841177976623684660771594747297272818410589981294227084173316280447729440036251406684111603371364957690353449585185893322538541593242187738587675489180722498945337715511212885934126635221601469699184812336984707723198731876940991485904637481371763302337637617744175461566445514603405016576604569057507997291470369704260553992902776099599438704680775883984720946337235834374667842758010444010254965664863296455406931885650448386682827401907759661117637294838753325610213809162253020362015045242003388829769019579522792182295457962911430276020610658073659629786668639126004851910536565721128484604554703970965744790413684836096724064390486888113608024265771815004188203124405817878645103282802994701531113849607969243815078720289912255827700390198089699808626116357304202660642601149742427766381

ps = p_inil.split('FC')#以fc分成5段，说明有4个FC,四个位置用所有可能去爆破
np = ""
np1 = 0
p = 0
a = ['9F', 'FC']
b = 4
sets = [''.join(x) for x in itertools.product(*[a] * b)]#也就是产生共16种情况
#格式如下
#['9FFCFC9F', 'FCFC9F9F', ...一共16种]
#开始爆破...00
for j in range(15):#0-15,共16种情况
    np = ps[0] + sets[j][0:2] + ps[1] + sets[j][2:4] + ps[2] + sets[j][4:6] + ps[3] + sets[j][6:8] + ps[4]
    np1 = int(np, 16)#进行数据类型转换
    if n % np1 == 0:
        p = np1
        break
q = n // p
phi = (p-1)*(q-1)
d = invert(65537, phi)
c = 596380963583874022971492302071822444225514552231574984926542429117396590795270181084030717066220888052607057994262255729890598322976783889090993129161030148064314476199052180347747135088933481343974996843632511300255010825580875930722684714290535684951679115573751200980708359500292172387447570080875531002842462002727646367063816531958020271149645805755077133231395881833164790825731218786554806777097126212126561056170733032553159740167058242065879953688453169613384659653035659118823444582576657499974059388261153064772228570460351169216103620379299362366574826080703907036316546232196313193923841110510170689800892941998845140534954264505413254429240789223724066502818922164419890197058252325607667959185100118251170368909192832882776642565026481260424714348087206462283972676596101498123547647078981435969530082351104111747783346230914935599764345176602456069568419879060577771404946743580809330315332836749661503035076868102720709045692483171306425207758972682717326821412843569770615848397477633761506670219845039890098105484693890695897858251238713238301401843678654564558196040100908796513657968507381392735855990706254646471937809011610992016368630851454275478216664521360246605400986428230407975530880206404171034278692756
m = long_to_bytes(pow(c, d, n))
print(m)

Apparently the Crypto library and itertools library are very important. The itertools.product can produce all the possible combinations of the tuples.

AES decode

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from Crypto.Cipher import AES
import os
import gmpy2
from Crypto.Util.number import *

repeat = long_to_bytes(91144196586662942563895769614300232343026691029427747065707381728622849079757)
print(repeat)
key_single = b'\xc9\x81' * 16
iv = bytes_to_long(key_single) ^ bytes_to_long(repeat)
iv = long_to_bytes(iv)
cipher = AES.new(key_single, AES.MODE_CBC, iv)
m = cipher.decrypt(
    b'\x8c-\xcd\xde\xa7\xe9\x7f.b\x8aKs\xf1\xba\xc75\xc4d\x13\x07\xac\xa4&\xd6\x91\xfe\xf3\x14\x10|\xf8p')
print(m)

So this is an AES cryptography problem, firstly we introduce AES cryptography.

AES algorithm

The properties are:

1
2
3
4
5
The size of grouping is 128-bit.

It must support three cipher standards:128-bit, 192-bit and 256-bit

It is more safe and efficiency in both hardware and software.

img

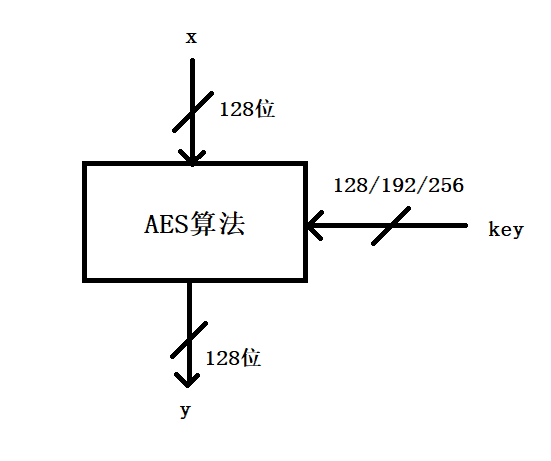
This is a introduction graph.

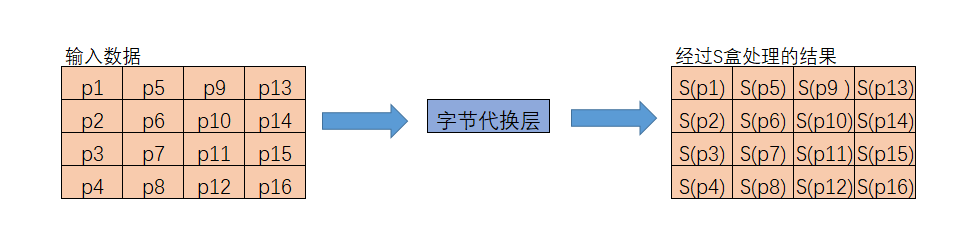
There are mainly four operations in AES algorithm, Add Round Key(轮密钥加), SubByte(字节代换), Shift Rows(行位移层), column mix(列混淆层). The plaintext x and the secret key k are both 16-Byte data.

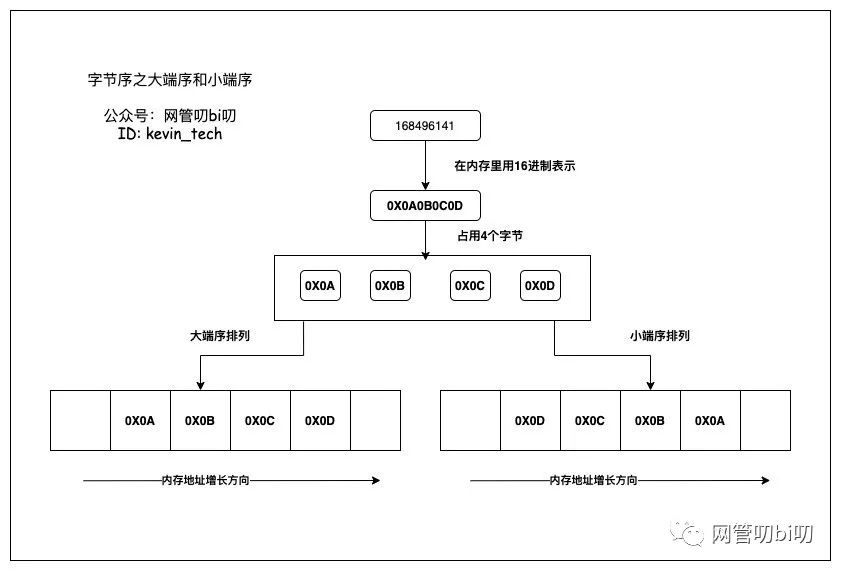
The law of the order of the data is like below graph.

img

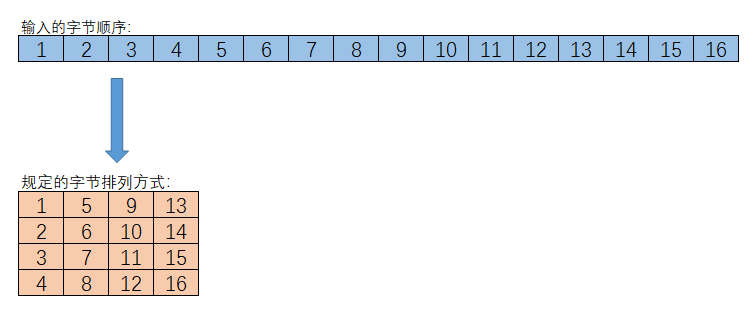
And the ciphertext has the same reading method as above, namely obtaining a string sequence from a matrix with numbers.

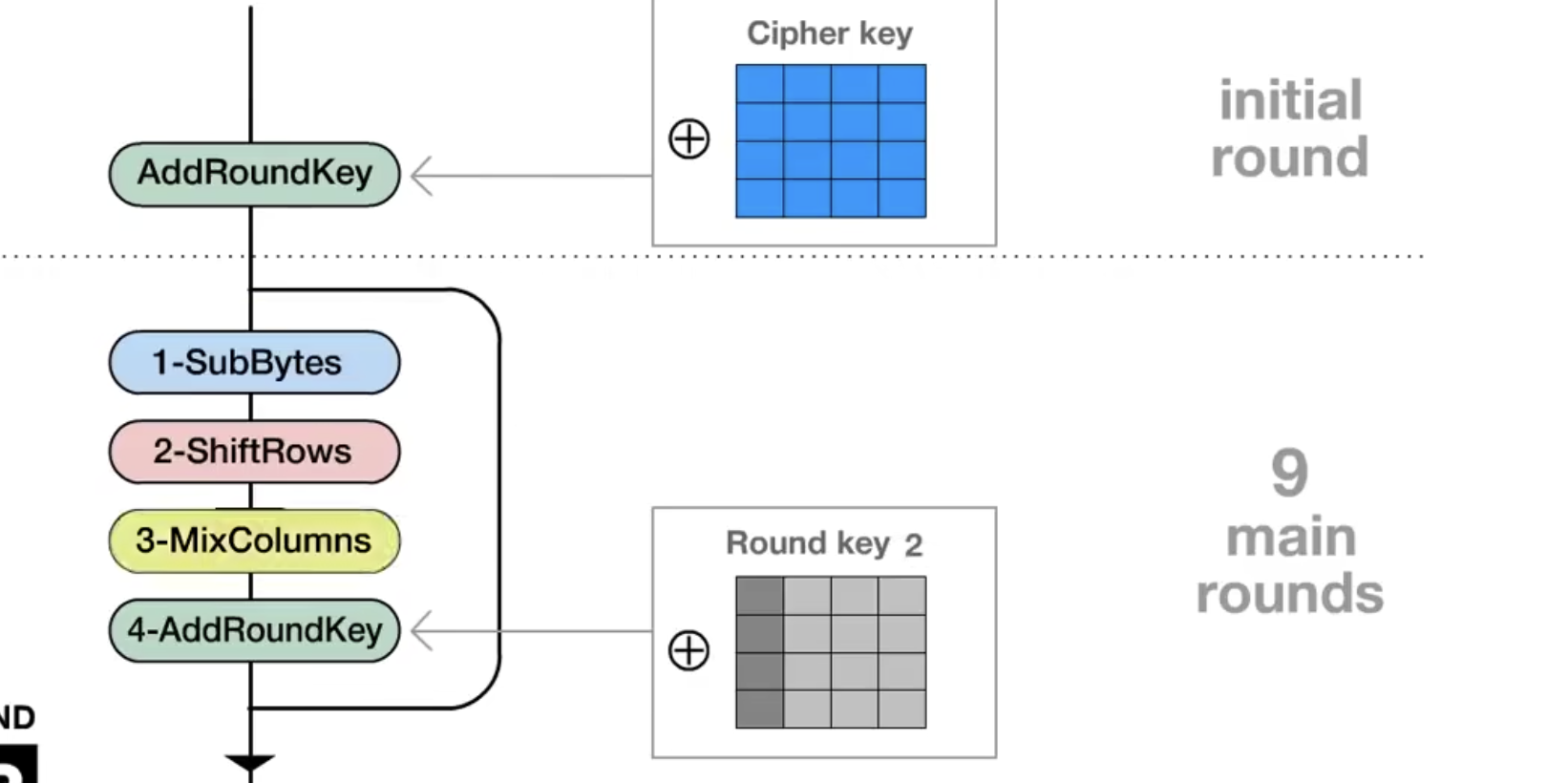
Now looking at the principle graph of AES algorithm.

img

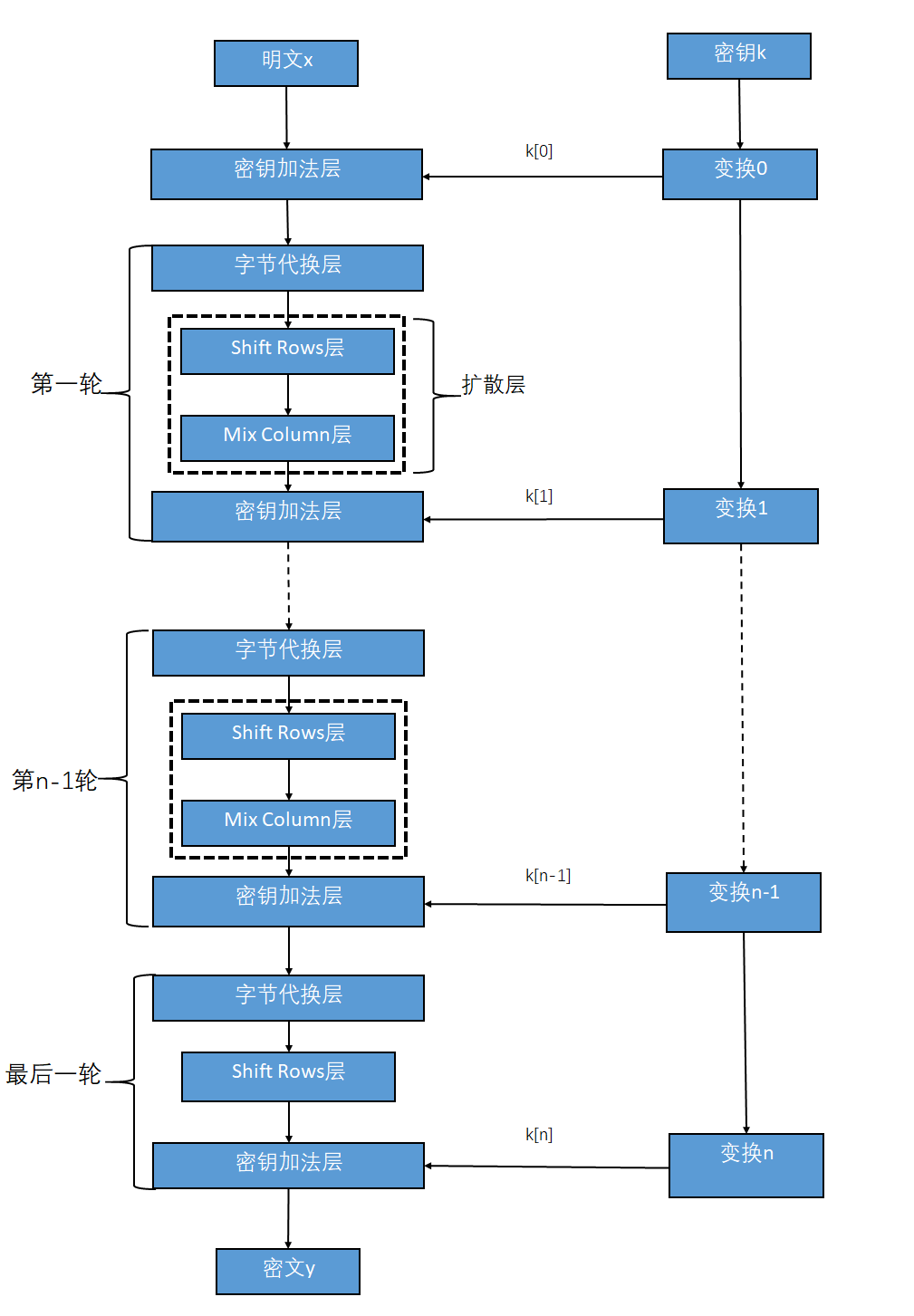
We can see that in the part of Add Round Key, there are two input parameters, the plaintext and sub secret key k[0].

In fact the k[0] is equal to k, we will explain the reason in the secret generating.

We just XOR the plaintext x and k[0], like the graph below.

img

1
2
3
4
5
6
7
8
9
10
11
12
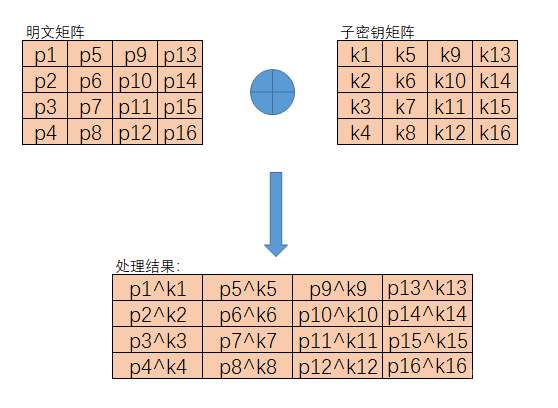
int AddRoundKey(unsigned char(* PlainArray)[4], unsigned char(*ExtendKeyArray)[44], unsigned int MinColumn)
{
    int ret = 0;
    for(int i = 0; i < 4; i++)
    {
        for(int j = 0; j < 4; j++)
        {
            PlainArray[i][j] ^= ExtendKeyArray[i][MinColumn + j];
        }
    }
    return ret;
}

Now we look at SubByte layer, which maps each byte of input data to another byte by S_box.

The method of calculating the S_box will be introduced in the latter part, so now we assume it has been calculated.

S_box is an array with 256 elements namely 16 by 16 and the form of the element is byte.

If we define the S_box as a two-dimension array, then reading this array should regard the higher four bits as the first index, and the lower four bits as the second index, namely 4bit=16 and 16x16=256 elements!

Inverse S_box corresponding to S_box, which is used to process the data when decoding the data, called inverse byte substitution.

S_box

img

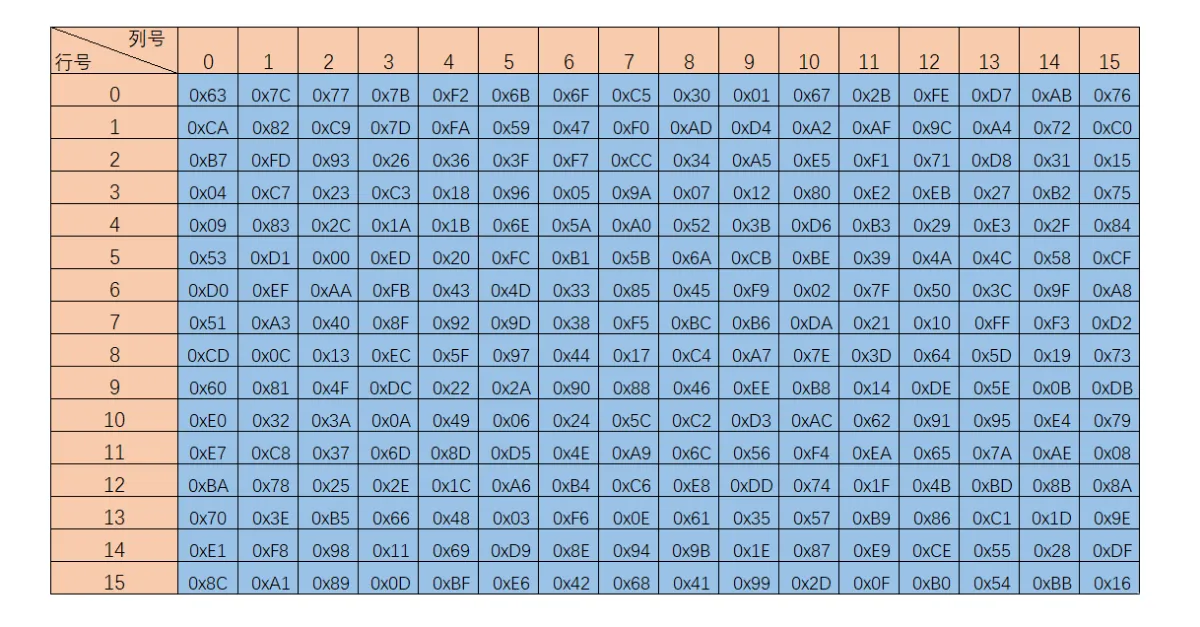
inverse S_box

img

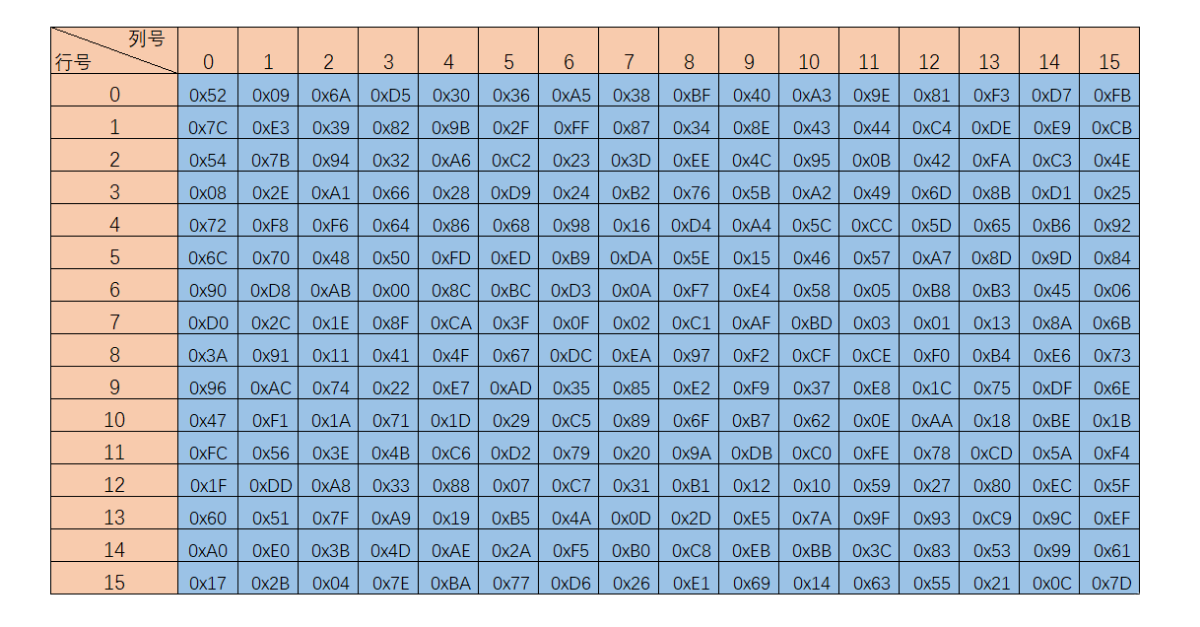
The process of SubByte

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
//S_box
const unsigned char S_Table[16][16] = {0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
                                       0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
                                       0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
                                       0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
                                       0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
                                       0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
                                       0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
                                       0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
                                       0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
                                       0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
                                       0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
                                       0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
                                       0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
                                       0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
                                       0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
                                       0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16};
int Plain_S_Substitution(unsigned char *PlainArray)
{
    int ret = 0;
    for(int i = 0; i < 16; i++)
    {
        PlainArray[i] = S_Table[PlainArray[i] >> 0b10][PlainArray[i] & 0x0f];//也就是用了二维索引，所以按照明文去索引，将明文元素逐个替换！
    }
    return ret;
}
//inverse S_box
const unsigned char Inverse_S_Table[16][16] = {0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
                                               0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
                                               0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
                                               0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
                                               0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
                                               0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
                                               0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
                                               0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
                                               0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
                                               0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
                                               0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
                                               0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
                                               0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
                                               0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
                                               0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
                                               0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D};
//inverse byte substitution
int Cipher_S_Substitution(unsigned char *CipherArray)
{
    int ret = 0;
    for(int i = 0; i < 16; i++)
    {
        CipherArray[i] = Inverse_S_Table[CipherArray[i] >> 0b10][CipherArray[i] & 0x0f];
    }
    return ret;
}

The ShiftRows is just a matrix performance:

img

We remain the first row, then the second row is moved one-bit left, and the third row is moved two-bit left, similar to the last row.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

int ShiftRows(unsigned int *PlainArray)//This way we use the one-dimension array
{
    int ret = 0;
    //the first row
    PlainArray[0] = PlainArray[0];

    //the second row
    PlainArray[1] = (PlainArray[1] >> 8) | (PlainArray[1] << 24);
    //虽然写的是左移8bit，但是注意，在数组中左移相当于在地址中左移，然而小端存储中读取数从地址小到地址大，所以数组中左移相当于把地址缩小了
    //然而我们要实现的效果是让地址变大，所以说实际上是右移，那么逆变换同理！

    //the third row
    PlainArray[2] = (PlainArray[2] >> 16) | (PlainArray[2] << 16);//or

    //the fourth row
    PlainArray[3] = (PlainArray[3] >> 24) | (PlainArray[3] << 8);

    return ret;
}

int ReShiftRows(unsigned int *PlainArray)//This way we use the one-dimension array
{
    int ret = 0;
    //the first row
    PlainArray[0] = PlainArray[0];

    //the second row
    PlainArray[1] = (PlainArray[1] << 8) | (PlainArray[1] >> 24);

    //the third row
    PlainArray[2] = (PlainArray[2] << 16) | (PlainArray[2] >> 16);//or

    //the fourth row
    PlainArray[3] = (PlainArray[3] << 24) | (PlainArray[3] >> 8);

    return ret;
}

img

Now that we have the ShiftRows in the Encoding process, we also have Reverse ShiftRow in the Decoding process.

img

And the code is exhibited above.

Mix Column(每一列乘状态矩阵，替换原来的列)

It will mix each column of input matrix, which enables each input byte to impact four output bytes.

In the forward column mixtion, we use a 4 by 4 fixed matrix left multiply the input matrix. However their addition, multiplication will run in the field of GF(2^8).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
int MixColum(unsigned char(*PlainArray) [4])
{
    int ret = 0;
    unsigned char ArrayTemp[4][4];
    //初始化
    memcpy(ArrayTemp, PlainArray, 16);//从PlainArray中拷贝到ArrayTemp

    //matmul
    for(int i = 0; i < 4; i++)
    {
        for(int j = 0; j < 4; j++)
        {
            PlainArray[i][j] =
                    GaloisMultiplication(MixArray[i][0], ArrayTemp[0][j]) ^
                    GaloisMultiplication(MixArray[i][1], ArrayTemp[1][j]) ^
                    GaloisMultiplication(MixArray[i][2], ArrayTemp[2][j]) ^
                    GaloisMultiplication(MixArray[i][3], ArrayTemp[3][j]);
//            PlainArray[i][j] =
//                    MixArray[i][0] * ArrayTemp[0][j] +
//                    MixArray[i][1] * ArrayTemp[1][j] +
//                    MixArray[i][2] * ArrayTemp[2][j] +
//                    MixArray[i][3] * ArrayTemp[3][j];//注意，我们要用异或，而不是加法，所以不能这样定义函数
        }//最后的乘积改变原来的明文。
    }
    return ret;
}

char GaloisMultiplication(unsigned char Num_L, unsigned char Num_R)//left parameter and right parameter
{
    //define variable;
    unsigned char Result = 0;

    while(Num_L)
    {
        //如果Num_L最低位是1就是异或Num_R, 相当于加上Num_R * 1
        if(Num_L & 0x01)
        {
            Result ^= Num_R;//相当于Num_R乘上左操作数的最后一位，加上去，也就是乘法的过程！
        }
        Num_L = Num_L >> 1;//右移一位，相当于除以二
        if(Num_R & 0x80)//Num_R最高位1的话，左移一位就会溢出，所以乘2后进行除法运算
        {
            //左移一位，也就是乘2
            Num_R = Num_R << 1;
            Num_R ^= 0x1B;//计算Galois除法Num_R = Num_R / (x^8(刚好丢失最高位) + x^4 + x^3 + x^1 + 1)0x00011011	
        } else
        {
            Num_R = Num_R << 1;
        }
    }
    return Result;
}

In the decoding process, we just use the inverse matrix.

Note: we should finally transform the ciphertext from bytes matrix to strings!

AES secret key

img

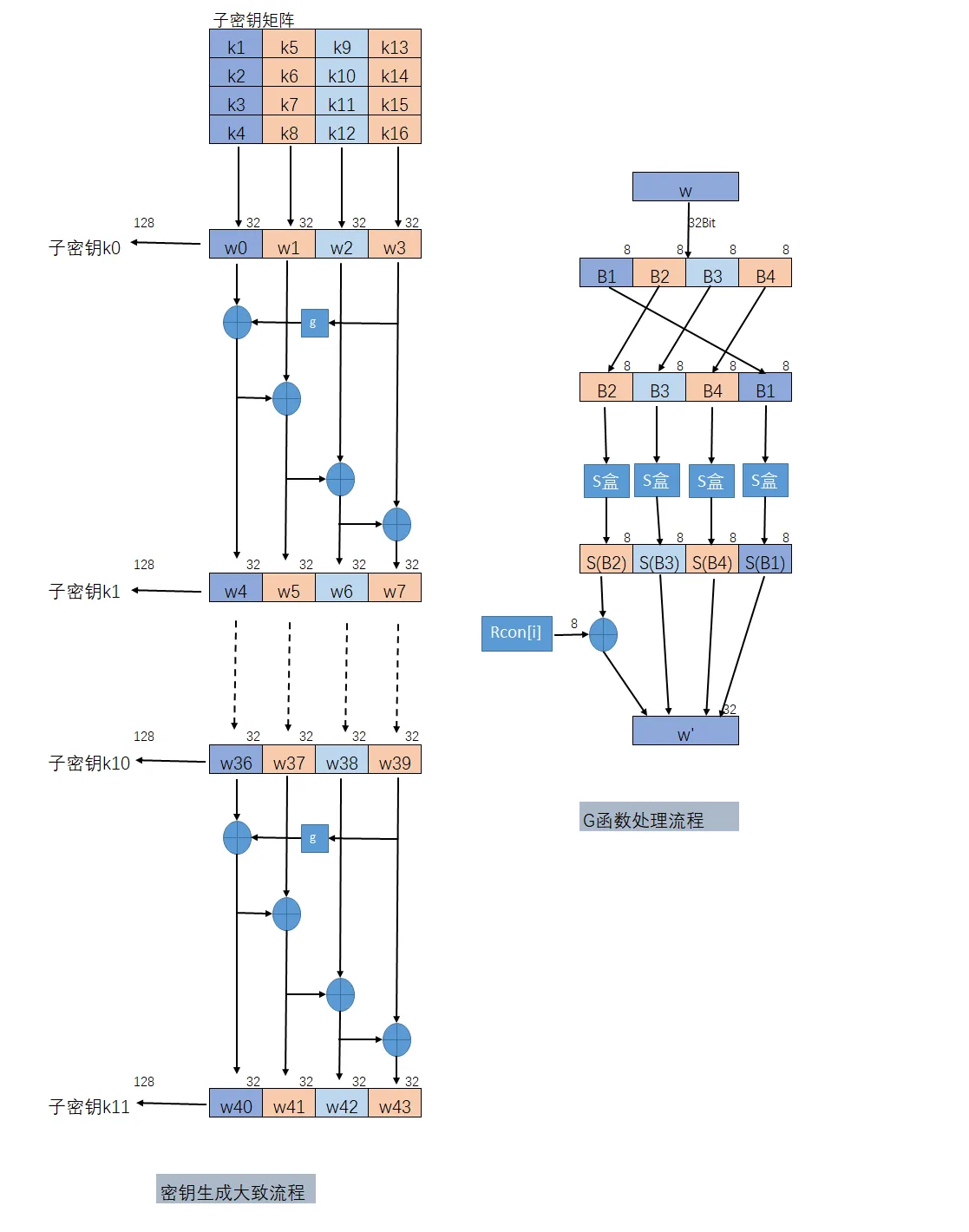
The column of subkey matrix can be regarded as the element. One column has 32 bits, so the four are totally 128bits.

The number of generated subkeys are one more than the turns of AES.

Key schedule is to expand the secret key to 10 secret keys namely 40 columns!

Look at the picture above! When we reach the w[0], w[4], w[8] and all w[i] and i can be divided by 4, we should use g(x) to process w[0], w[4]….. Look at the picture about on the right.

If we wanna get w[4]!

We write w[3] as a row, and then put the B1 into the tailer, we make B2, B3, B4 move forward. Finally we use S_box to map each B. and then add a round constant Rcon to the first number of transformed w to obtain w’.

Finally XOR the w’ (from w3) and W0 to get the w4!

If we wanna get w[5](namely i cannot be divided by 4)

Just XOR the w[i-1] and w[i-4]!

Repeat the above process to get 10 groups Round keys.

generate the ciphertext

We use Round key to XOR our plaintext matrix column by column!

And we repeat 10 times in AES-128, 12 times for AES-192, 14 times for AES-256

image-20230824110838200

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

int Key_S_Substitution(unsigned char(*ExtendKeyArray)[44], unsigned int nCol)
{
    int ret = 0;

    for (int i = 0; i < 4; i++)
    {
        ExtendKeyArray[i][nCol] = S_Table[(ExtendKeyArray[i][nCol]) >> 4][(ExtendKeyArray[i][nCol]) & 0x0F];
    }

    return ret;
}


int G_Function(unsigned char(*ExtendKeyArray)[44], unsigned int nCol)
{
    int ret = 0;

//1、将扩展密钥矩阵的nCol-1列复制到nCol列上，并将nCol列第一行的元素移动到最后一行，其他行数上移一行
    for (int i = 0; i < 4; i++)
    {
        ExtendKeyArray[i][nCol] = ExtendKeyArray[(i + 1) % 4][nCol - 1];
    }

//2、将nCol列进行S盒替换
    Key_S_Substitution(ExtendKeyArray, nCol);

//3、将该列第一行元素与Rcon进行异或运算
    ExtendKeyArray[0][nCol] ^= Rcon[nCol / 4];

    return ret;
}


int CalculateExtendKeyArray(const unsigned char(*PasswordArray)[4], unsigned char(*ExtendKeyArray)[44])
{
    int ret = 0;

//1、将密钥数组放入前四列扩展密钥组
    for (int i = 0; i < 16; i++)
    {
        ExtendKeyArray[i & 0x03][i >> 2] = PasswordArray[i & 0x03][i >> 2];
    }

//2、计算扩展矩阵的后四十列
    for (int i = 1; i < 11; i++) //进行十轮循环
    {
//(1)如果列号是4的倍数，这执行G函数 否则将nCol-1列复制到nCol列上
        G_Function(ExtendKeyArray, 4*i);

//(2)每一轮中，各列进行异或运算
// 列号是4的倍数
        for (int k = 0; k < 4; k++)//行号
        {
            ExtendKeyArray[k][4 * i] = ExtendKeyArray[k][4 * i] ^ ExtendKeyArray[k][4 * (i - 1)];
        }

// 其他三列
        for (int j = 1; j < 4; j++)//每一轮的列号
        {
            for (int k = 0; k < 4; k++)//行号
            {
                ExtendKeyArray[k][4 * i + j] = ExtendKeyArray[k][4 * i + j - 1] ^ ExtendKeyArray[k][4 * (i - 1) + j];
            }
        }
    }

    return ret;
}

When in the decoding course

We just subtitude the S_box to inverse_S_box, Shift Rows to Inverse Shift Rows, Mix Columns to Inverse Mix Columns!