第二章 数字图像基础

2.4 图像取样和量化

1.取样和量化基本概念

取样是空间离散化，量化是幅值离散化。

量化是将f(x, y)的连续分布的值划分为若干个字空间，在同一字空间内的不同灰度值都用这个空间内某一个确定值代替，形成一个有限可列数值序列。

显然，量化误差就是有限个离散值近似表示无限多个连续值产生的误差，也叫量化失真。

image-20231005110112497

2. 数字图像的表示

image-20231005110141841

我们可以用双函数来表示像素，其中两个参数就是像素的坐标。

其中,M, N必须是整数，有时候将灰度的取值范围称为图像的动态范围，将占灰度级的全部有效段的图像叫做高动态范围图像。

存储数字图像的比特数为$b = M \times N \times k$，当一幅图像有$2^k$个灰度级时，则该图像是k比特图像。

比如黑白图像，有256个灰度级，即$2^8$个，$k = 8$。

空间分辨率：图像中可辨别的最小细节。单位:dpi(dots per inch)单位距离内的像素数。

灰度分辨率：灰度级中可辨别的最小变化。单位:bit，用于量化灰度的比特数。

image-20231005111426078

这是256灰度，而下图，是4灰度。

image-20231005111450159

并且，对于大量细节图像，只需要较少的灰度等级。

4. 图像内插

即重采样。由已知像素数估计未知像素的像素灰度。

比如坐标关系：

词向量(Word2Vec)

简要来说就是把词汇用向量来表示，一般是行向量，每一列表示一个特征，通常想精确描述词汇所有特征，大概需要50-300维向量，这也是我们通常定义一个词向量的维度范围。但实际上向量是降维之后的结果，我们看到的经过降维的结果已经不能逐列分析其含义了。

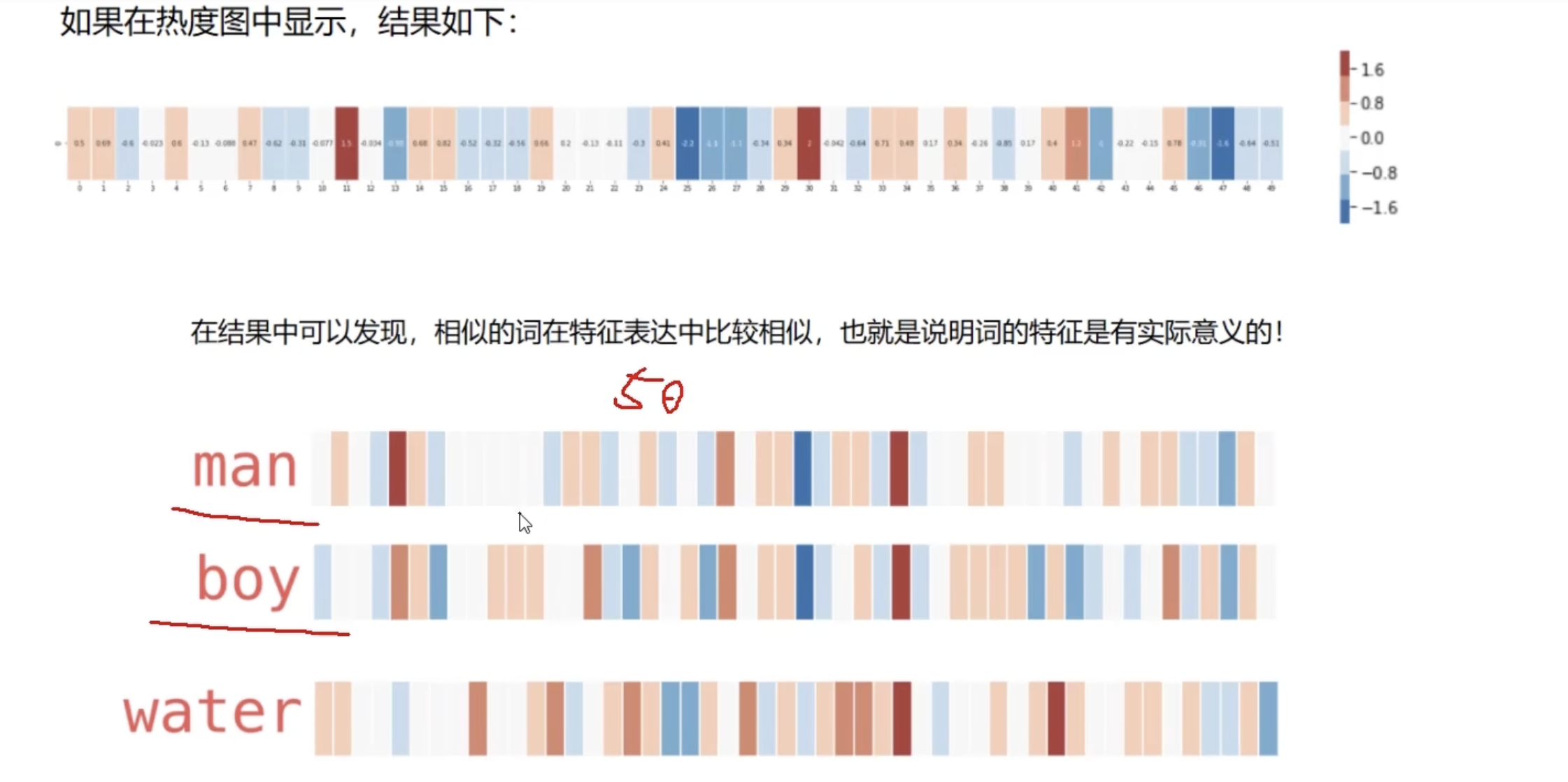
image-20240114184038151

可以用热度图来表示词向量中每一项的大小。

实际上我们的RNN模型，应用于自然语言处理，就是想预测下一个词是什么，如图所示。

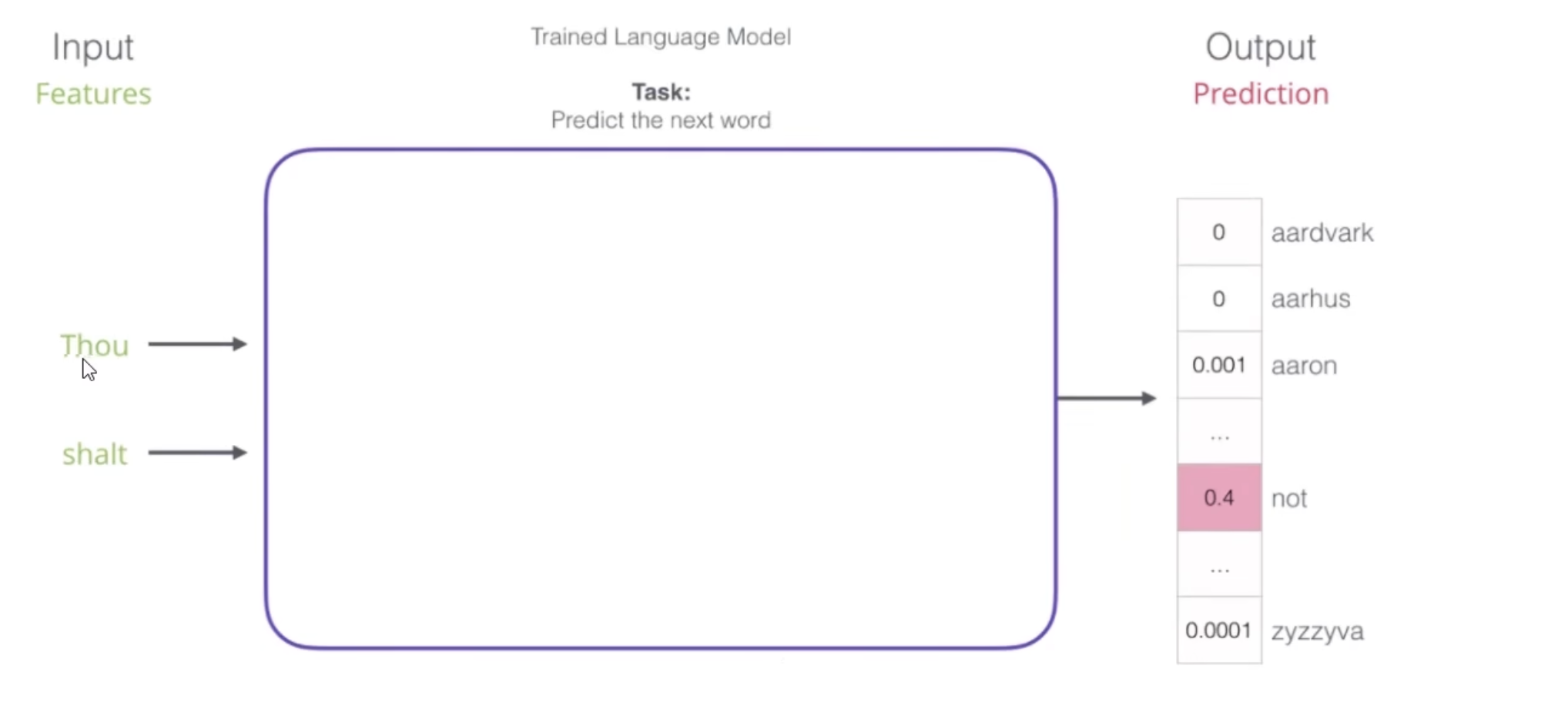
image-20240114185015139

得到下一个可能得词汇的概率。

中间的结构如图所示：

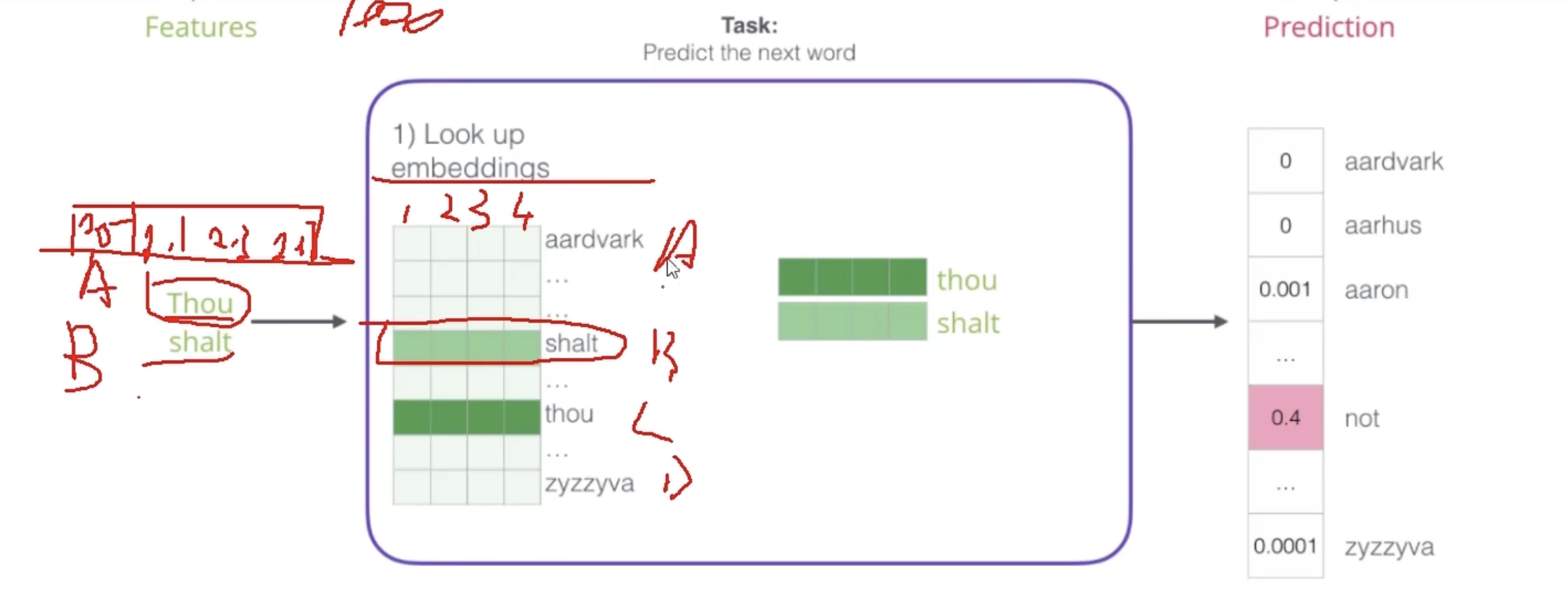
image-20240114192839499

首先是查表，也就是查对应的词向量。当然这个表哪来的呢，一开始我们随机初始化所有的向量，我们知道在深度学习模型中前向传播计算Loss function，反向传播利用loss function更新权重参数，

随着训练进行，每次都会把表进行更新，使得loss更小。

我们可以这样构造数据集，如图所示：

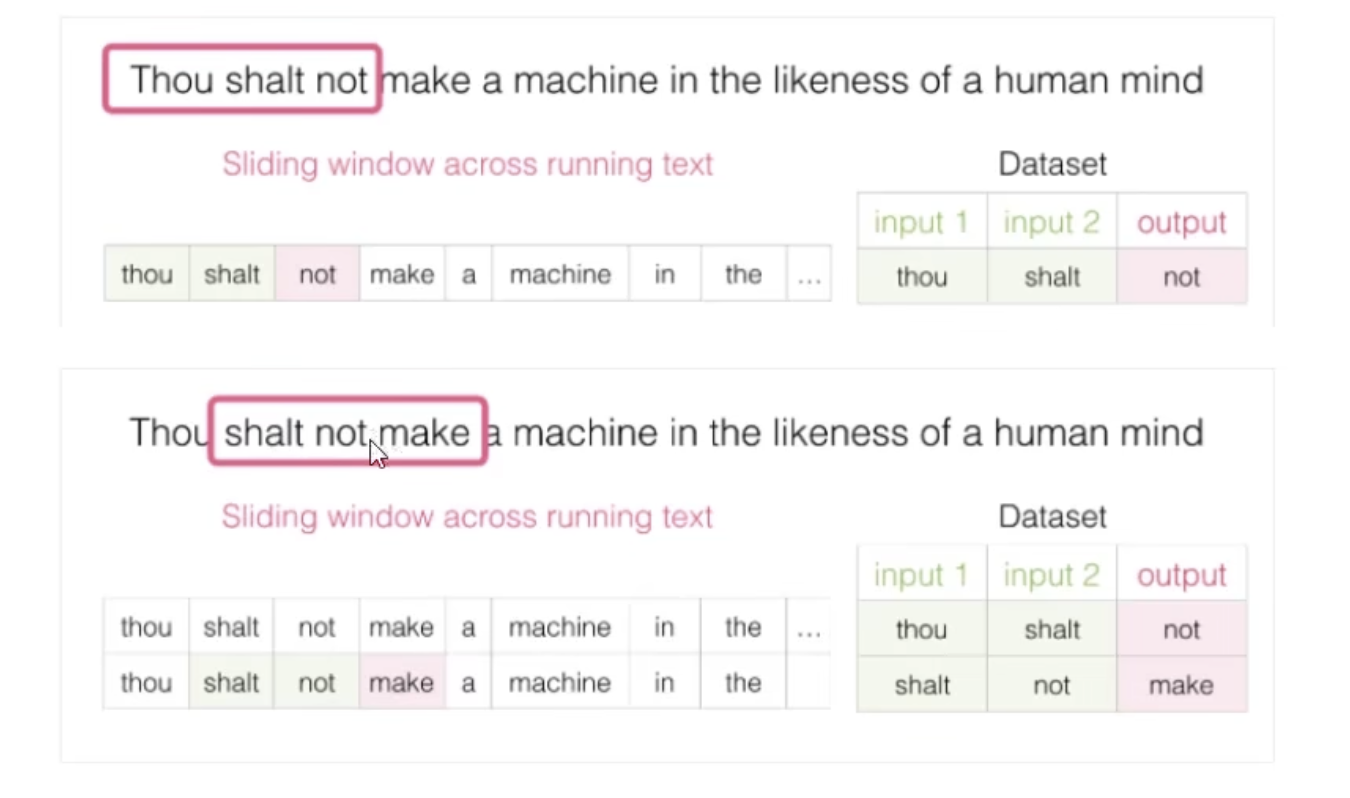
image-20240114201431903

一次一次滑动形成输入输出数据集。

caffe中的prototxt文件解读

这个文件一般用来存储模型，或者说网络的架构。

架构中含有每一层网络的具体参数，参考这个链接https://blog.csdn.net/github_37973614/article/details/81810327

我们补充一个重要的东西就是im2col层，用来帮助卷积运算。

img

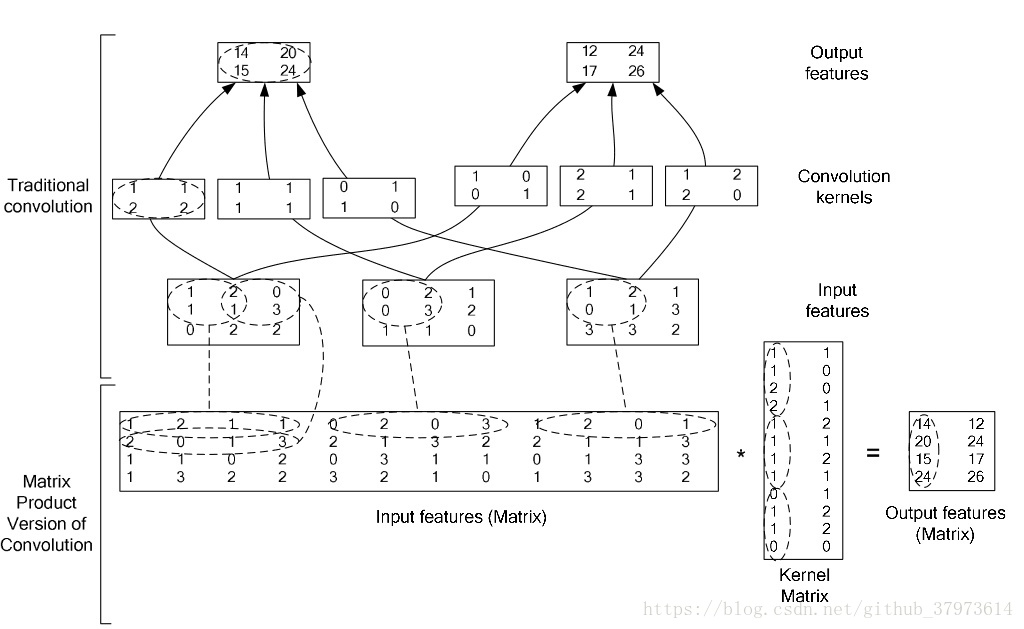
可以看到将一个图片，按照卷积核的大小来框成一个新矩阵，也就是左下角矩阵，其中每一列代表一个图片。

可以看到输入是1x3x3x3(NxCxHxW)，而卷积核是2x3x2x2(NxCxHxW)，所以输出肯定有两个batch，然后每一个都是卷积核大小也就是2x2，而右下角为im2col之后的输出形式，显然包含了我们所需要的输出特征，也就是两层，每一层向量长度是4。

image-20240123015729530

对于这个prototxt文件中的reshape层，其中，shape{}里面分别会标注第一维一直到最后一维的维数，如果是正数的话，那么正数就是维数，比如dim=2处索引是1，而索引1表示第二个维度，所以dim=2这一行就是第二个维度的维数是2。dim=0表示与bottom也就是输入层对应维度的维数相同。dim=-1就是别的都算完了，用元素总数除以其他维度乘积，算出最后维度。比如矩阵展开了一共24个元素，原来矩阵的第一维是2，其他都按照图中标注来算，那么输出矩阵的大小就应该是2x2x3x2即可。

1
2
3
4
5
6
7
8
If "input" is 2D with shape 2 x 8, then the following reshape_param
  // specifications are all equivalent, producing a 3D blob "output" with shape
  // 2 x 2 x 4:
  //
  //   reshape_param { shape { dim:  2  dim: 2  dim:  4 } }
  //   reshape_param { shape { dim:  0  dim: 2  dim:  4 } }
  //   reshape_param { shape { dim:  0  dim: 2  dim: -1 } }
  //   reshape_param { shape { dim:  0  dim:-1  dim:  4 } }

如果只有

1
2
3
4
shape{
	dim=0
	dim=-1
}

那么就和展开一样的，也称和展平层（flatten layer）相同。

下面是额外参数axis

1
2
3
4
5
6
7
8
9
10
11
12
// axis may be non-zero to retain some portion of the beginning of the input
// shape (and may be negative to index from the end; e.g., -1 to begin the
// reshape after the last axis, including nothing in the reshape,
// -2 to include only the last axis, etc.).
//
// For example, suppose "input" is a 2D blob with shape 2 x 8.
// Then the following ReshapeLayer specifications are all equivalent,
// producing a blob "output" with shape 2 x 2 x 4:
//
//   reshape_param { shape { dim: 2  dim: 2  dim: 4 } }
//   reshape_param { shape { dim: 2  dim: 4 } axis:  1 }
//   reshape_param { shape { dim: 2  dim: 4 } axis: -3 }

对于num_axes，稍微有点难理解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// num_axes specifies the extent of the reshape.
  // If num_axes >= 0 (and axis >= 0), the reshape will be performed only on
  // input axes in the range [axis, axis+num_axes].
  // num_axes may also be -1, the default, to include all remaining axes
  // (starting from axis).
  //
  // For example, suppose "input" is a 2D blob with shape 2 x 8.
  // Then the following ReshapeLayer specifications are equivalent,
  // producing a blob "output" with shape 1 x 2 x 8.
  //
  //   reshape_param { shape { dim:  1  dim: 2  dim:  8 } }
  //   reshape_param { shape { dim:  1  dim: 2  }  num_axes: 1 }
  //   reshape_param { shape { dim:  1  }  num_axes: 0 }
  //
  // On the other hand, these would produce output blob shape 2 x 1 x 8:
  //
  //   reshape_param { shape { dim: 2  dim: 1  dim: 8  }  }
  //   reshape_param { shape { dim: 1 }  axis: 1  num_axes: 0 }

这是表示重塑的范围，就是只有[axis, axis + num_axes]的范围才会被重塑，其余范围不变！

我们就看最后一个例子，想要表示2x1x8，最后一行中，给出了一个dim=1，但是后面给出axis=1和num_axes=0，也就是说只有[1]这个维度才会被重塑，重塑成dim=1，而[1]是第二维，所以dim=1并不是指第一维变成1，因为第一维变成1就无法实现我们想要的输出2x1x8了，只有第二维变成1，然后根据nun_axes性质，其余维度不变，最终结果大小为2x1x8。