整数规划

割平面法

引入松弛变量达到原来的效果。

下面介绍割平面法基本步骤：

如图所示，也就是说整数和整数在一起，小数和小数在一起。所以说最后一个式子右边应该小于等于0，所以直接得到一个整数约束方程。

下面是程序框图

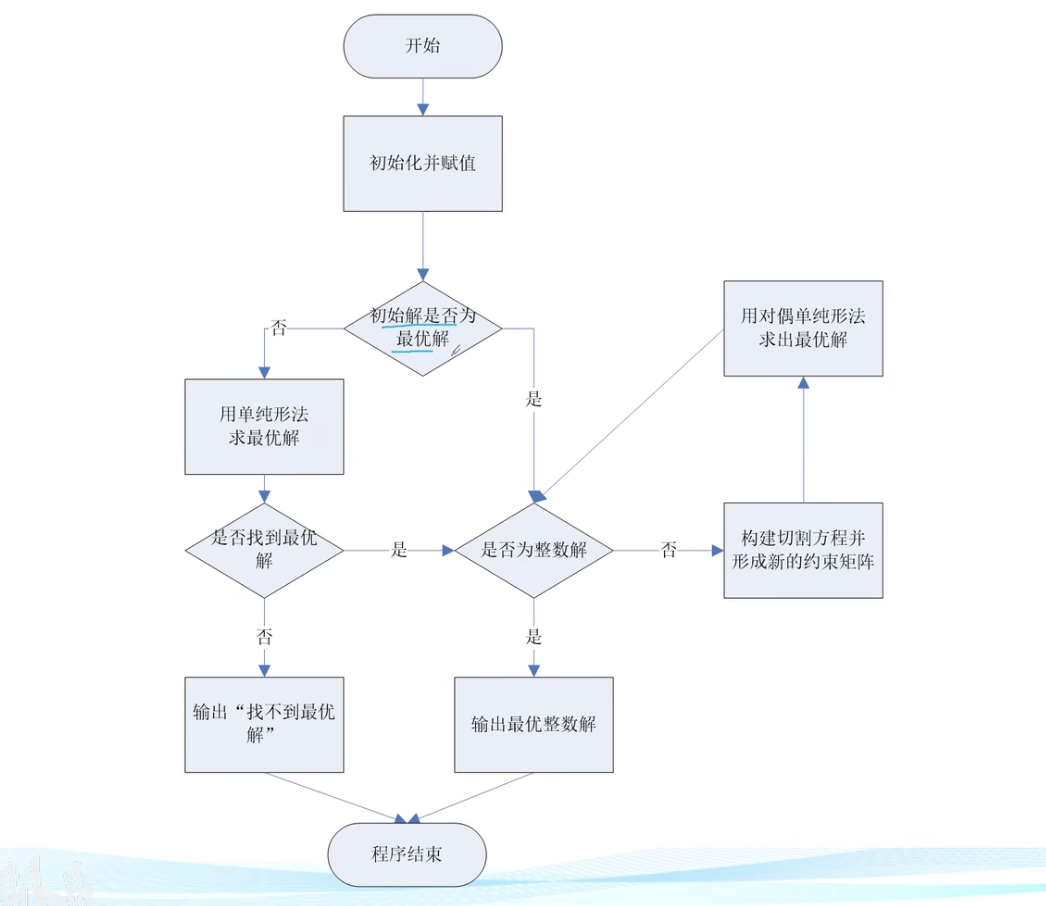
看下面例题：

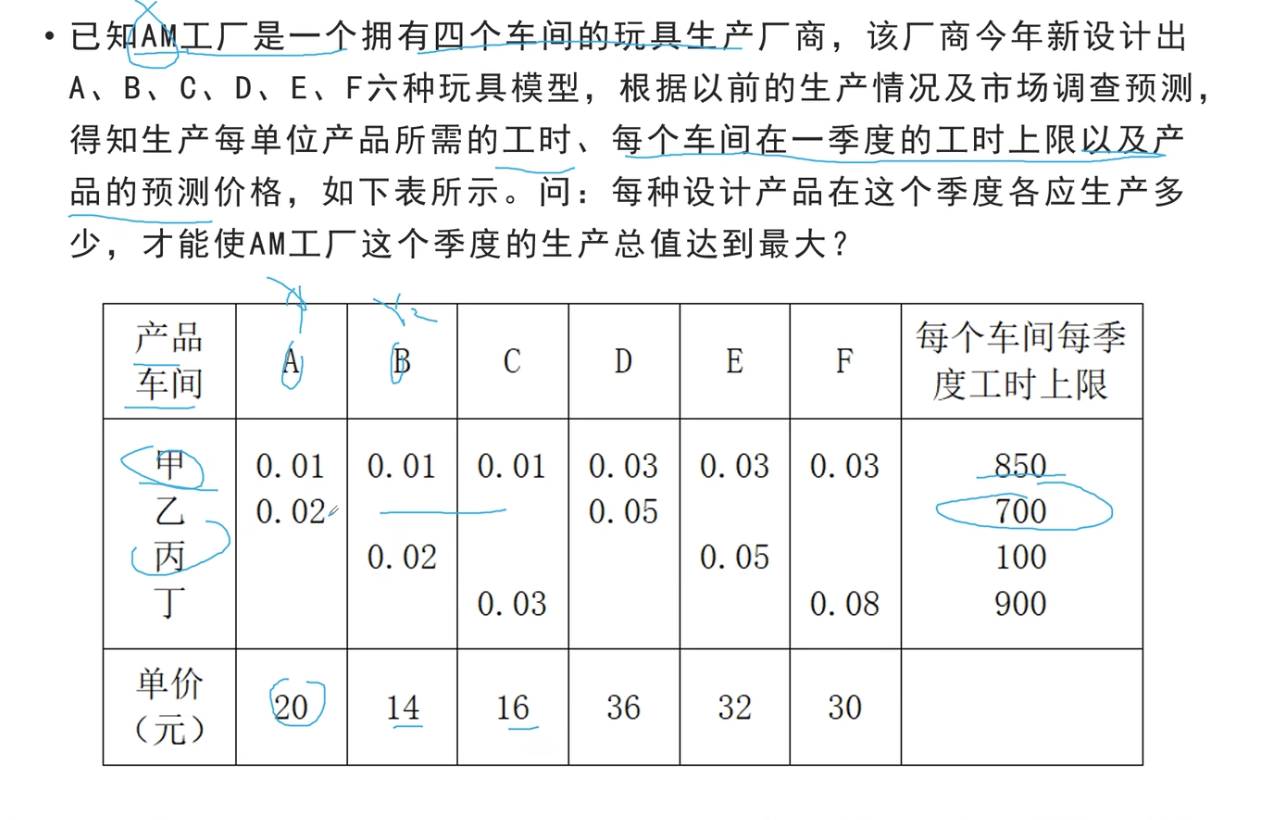
显然我们直接列式子

匈牙利法

下面看0-1变量的使用

下面看基于0-1的互斥约束问题。

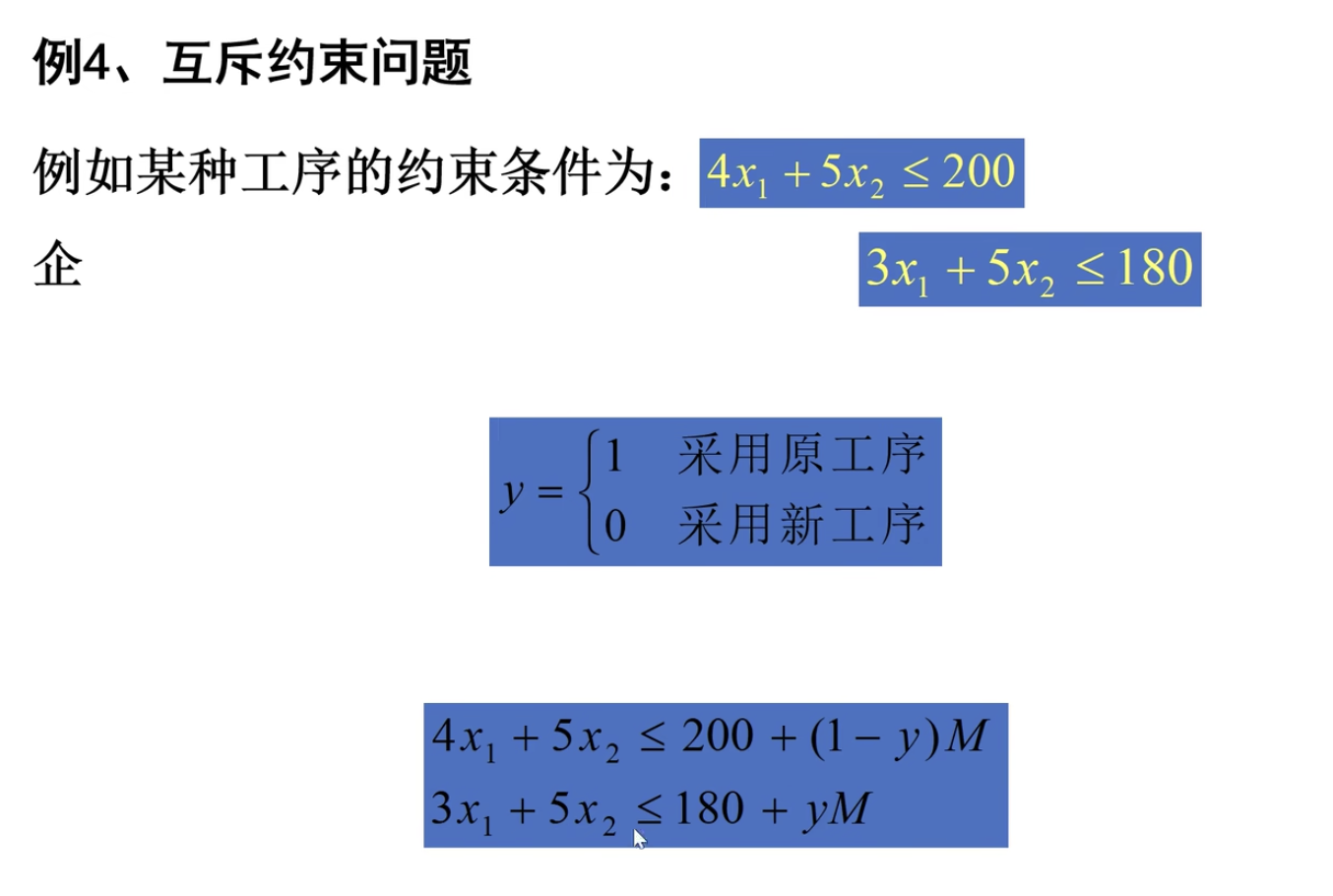
取M为接近无穷大即可让另一个条件失效，保持一个条件成立，妙。

下面是互斥作用的推广：

当我们不选Yi时，就置1，也就是一共p个，减去不选的yi个，就剩下选的q个，所以p-q就是yi的和。并且如果不选的话，第一行M的无穷大效果就会体现，让第一个式子直接失效！妙！

看下面例题（固定费用问题）

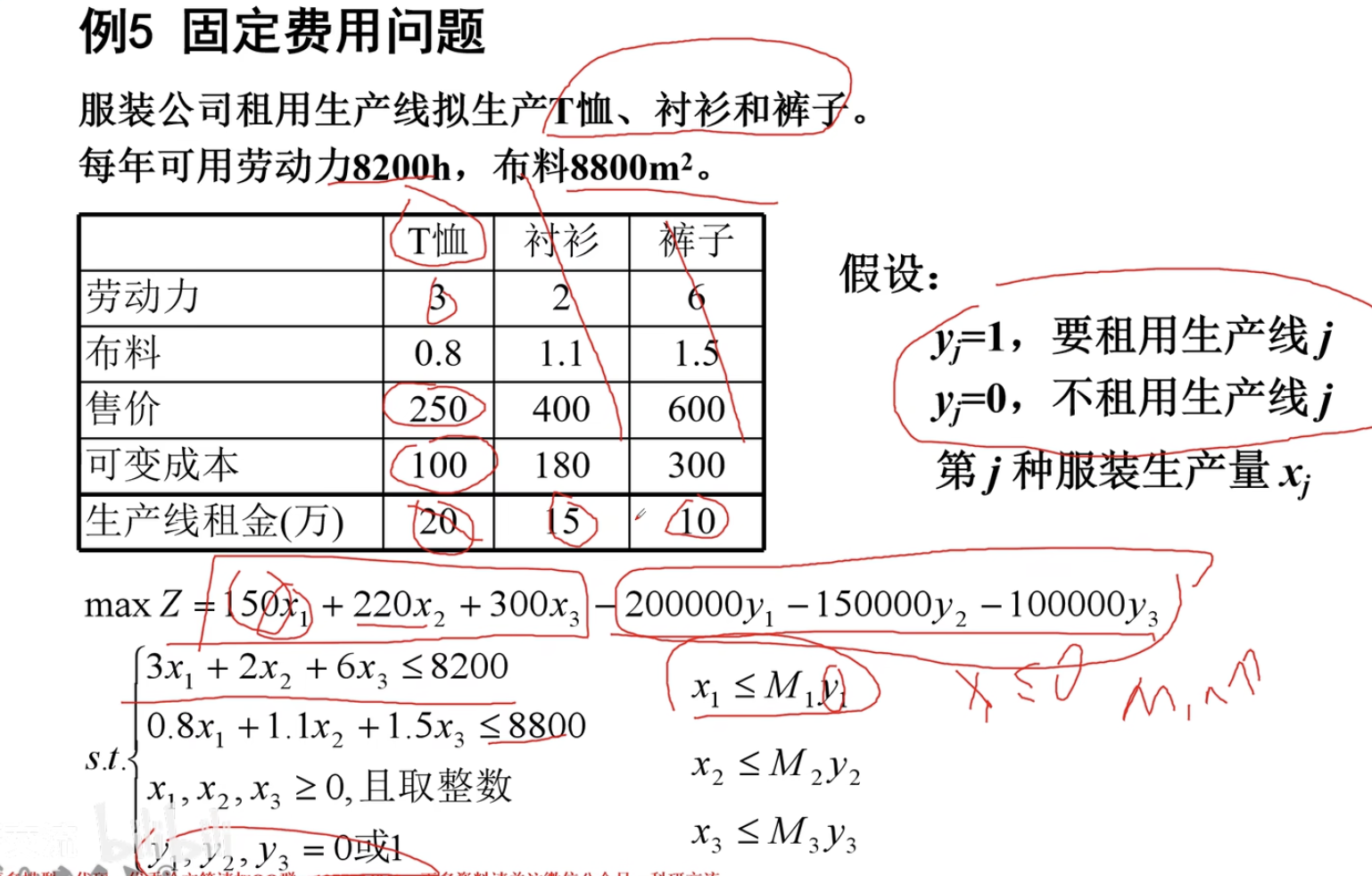
也就是当$x_1 \le M_iy_i$时可以看到，此时如果选用此条生产线也就是$y_i$取1，那么$M_i$的无穷效果触发，对应的$x_1$就无所谓了。

指派问题

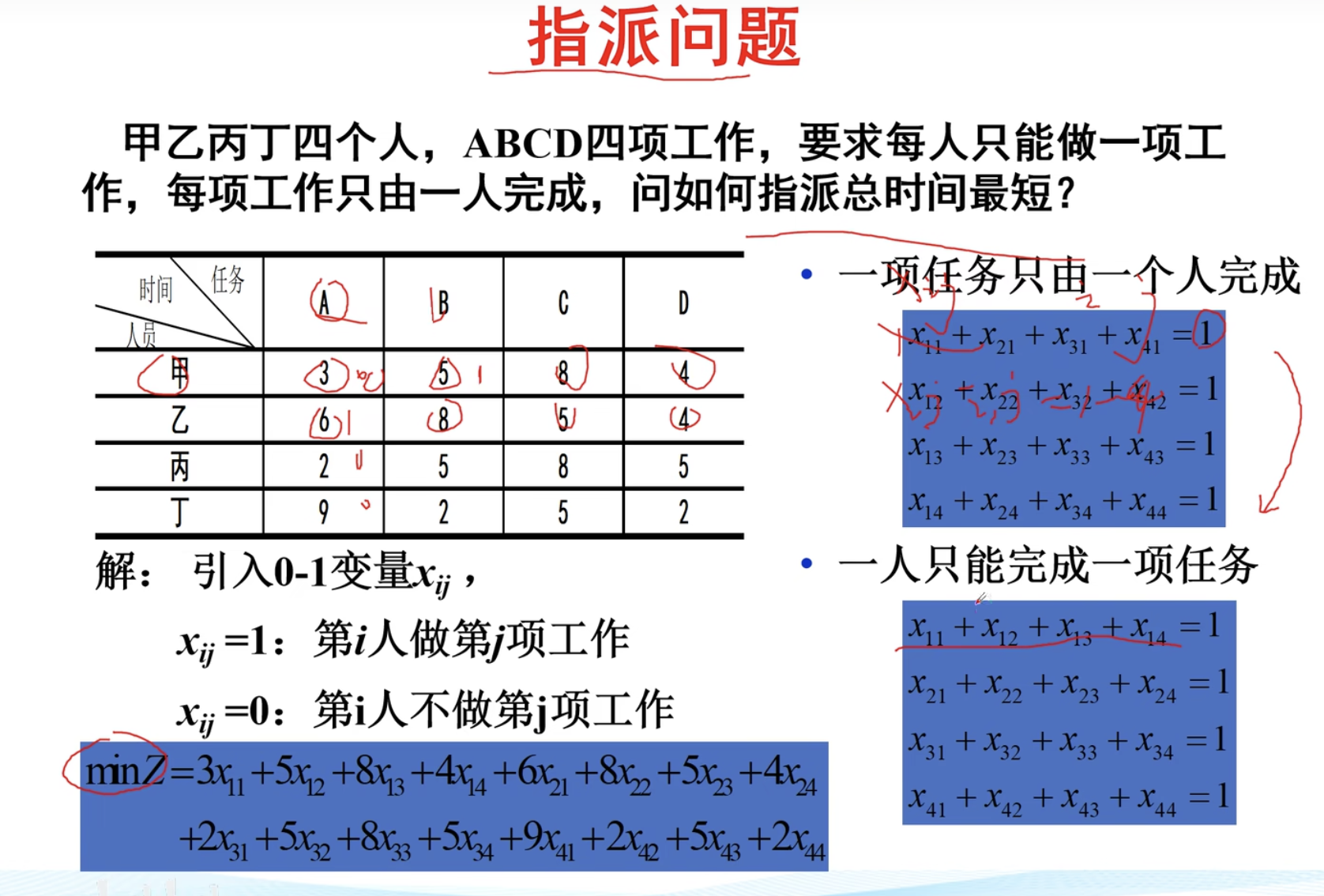
出现一个系数矩阵，有n个人和n项工作。

看标准形式：

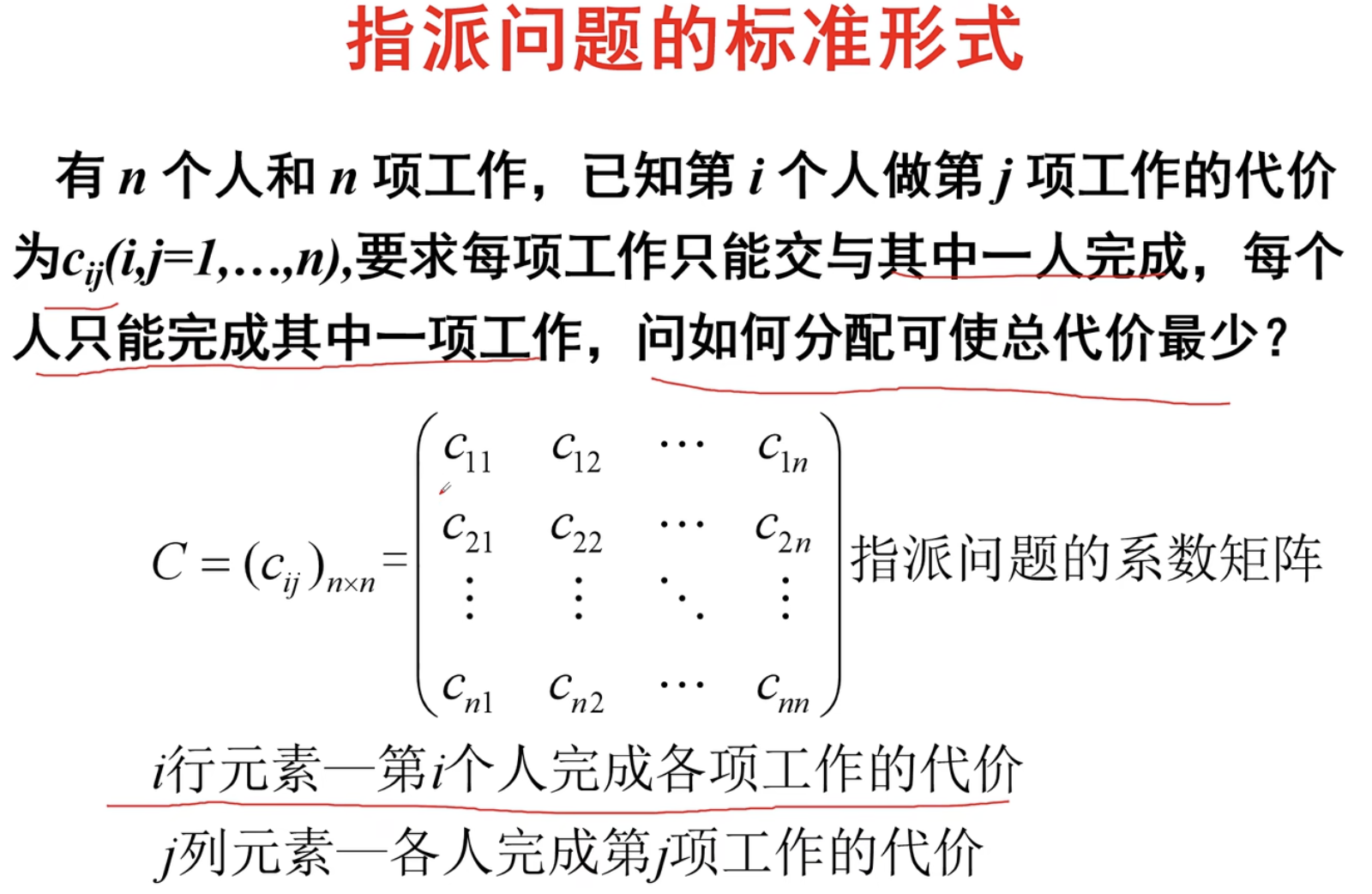
既然有系数矩阵，也就有解矩阵

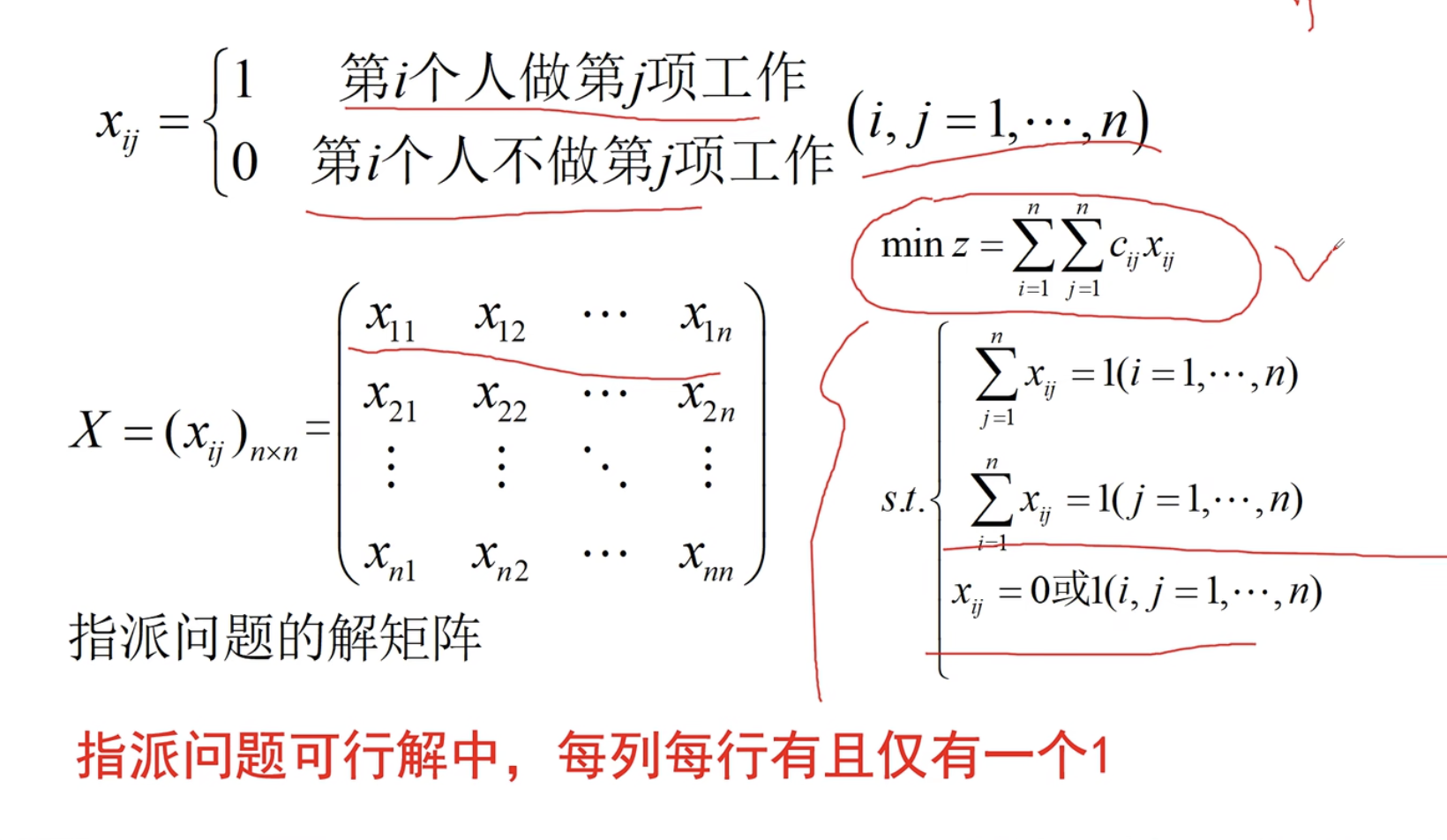
每一行和每一列只能有一个1，也就是一个人只能完成一项工作，

一项工作只能有一个人去做，一一对应即可！然后看她们的最大效率。

也会有以下最大化指派问题

只需要找到反过来的系数即可，也就是

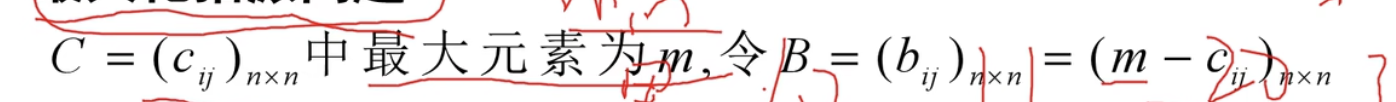
还会有其他情况，比如人数和工作数不等

下面进入正题：

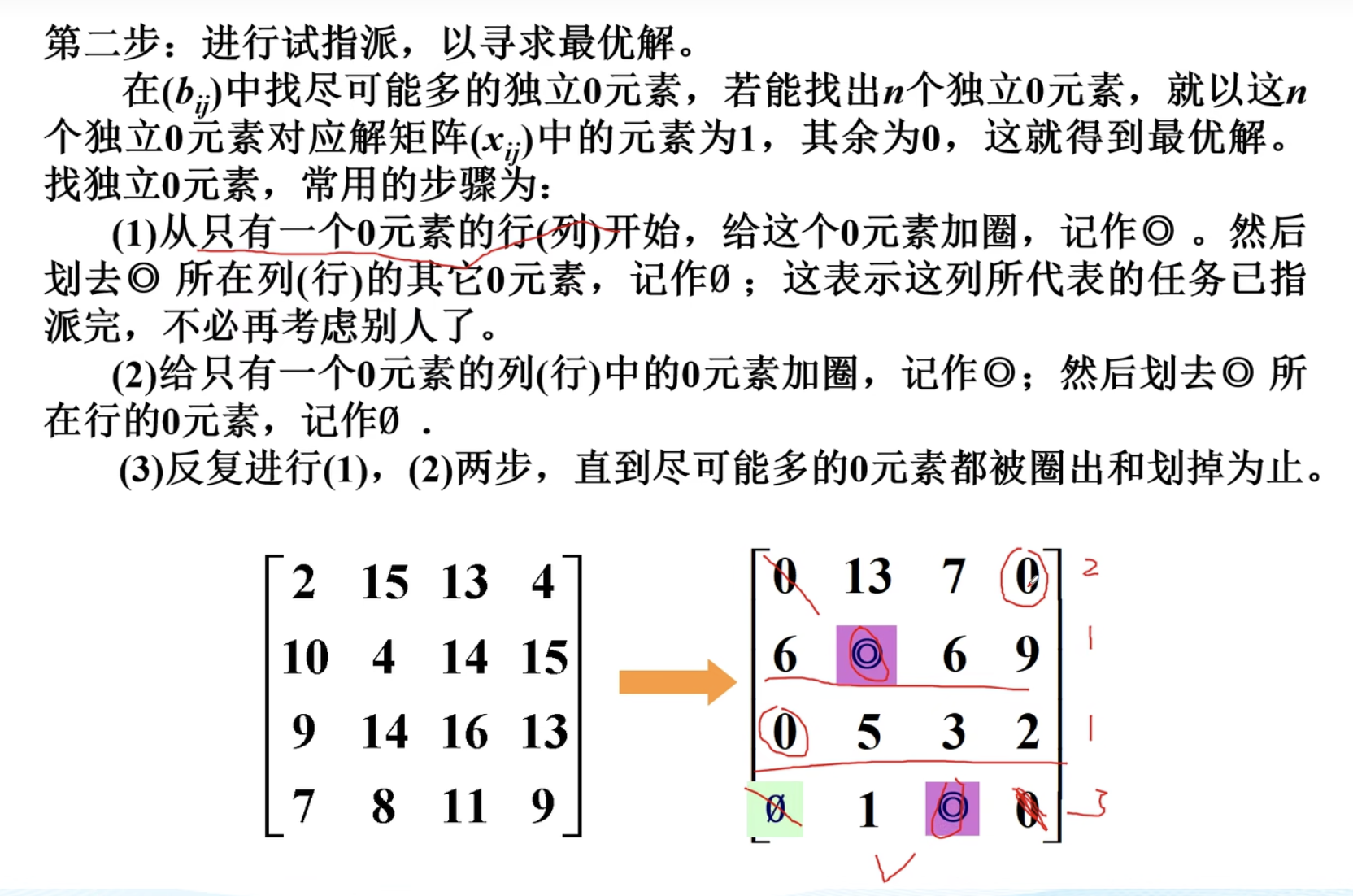
指派问题的匈牙利解法的一般步骤

其实就是构造出$b_{ij}$矩阵使得其为列满秩矩阵并且只有0和1。

行减去最小元素生成0，列也是如此。

通过先分配成本最低的生厂商及任务，然后划掉这一列其他的0，也就是说这一个任务只有此一个人做，已经把人确定了，不能有其他人了。其他同理。最后转换为解矩阵时把这些独立0元素转换为1即可得到$b_{ij}$

下面是特殊情况，就是一行多个零的时候。

下面来一个矩阵我们自己动手化一下

代码部分见网盘。